题目内容
【题目】在数列{an}中，已知a1= 
，an+1= an﹣ 
，n∈N* ， 设Sn为{an}的前n项和．
（1）求证：数列{3nan}是等差数列；
（2）求Sn；
（3）是否存在正整数p，q，r（p＜q＜r），使Sp ， Sq ， Sr成等差数列？若存在，求出p，q，r的值；若不存在，说明理由．
【答案】
（1）证明：由an+1= 
an﹣ 
，n∈N*，
得到3n+1an+1=3nan﹣2，
则3n+1an+1﹣3nan=﹣2．
又∵a1= ，
∴3×a1=1，
数列{3nan}是以1为首项，以﹣2为公差的等差数列
（2）解：由（1）可以推知：3nan=1﹣2（n﹣1），
所以，an= 
，
所以Sn= ﹣ 
﹣ 
﹣ 
﹣…﹣ ，①
Sn= ﹣ 
﹣ 
﹣ 
﹣…﹣ 
，②
①﹣②，得
Sn= ﹣2（ + + 
+…+ 
）﹣ ，
= ﹣2×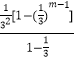 
﹣ ，
= 
，
所以Sn= 
（3）解：假设存在正整数p，q，r（p＜q＜r），使Sp，Sq，Sr成等差数列．
则2Sq=Sp+Sr，
即 
= 
+ 
．
由于当n≥2时，an= ＜0，
所以数列{Sn}单调递减．
又p＜q，
所以p≤q﹣1且q至少为2，
所以 ≥ 
， ﹣ = 
．
①当q≥3时， ≥ ≥ ，
又 ＞0，
所以 ＜ + ，等式不成立．
②当q=2时，p=1，
所以 
= + ．
所以 = 
，
所以r=3，（数列{Sn}单调递减，解唯一确定）．
综上可知，p，q，r的值分别是1，2，3
【解析】（1）把给出的数列递推式an+1= an﹣ ，n∈N* ， 变形后得到新数列{3nan}，该数列是以1为首项，以﹣2为公差的等差数列；（2）由（1）推出{an}的通项公式，利用错位相减法从而求得求Sn；（3）根据等差数列的性质得到2Sq=Sp+Sr ， 从而推知p，q，r的值．
【考点精析】利用等差关系的确定和数列的前n项和对题目进行判断即可得到答案，需要熟知如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，即
－
=d ，（n≥2，n∈N
）那么这个数列就叫做等差数列；数列{an}的前n项和sn与通项an的关系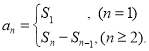
．
