题目内容
 求图中阴影部分绕轴旋转所成旋转体的全面积和体积.
求图中阴影部分绕轴旋转所成旋转体的全面积和体积.分析:几何体是图中阴影部分绕直线l旋转一周所得旋转体,是一个圆台内挖去一个球后剩余部分,求出圆台的表面积加上球的表面积,可得几何体的体积;求出圆台的体积减去球的体积,可得几何体的体积.
解答: 解:如图所示,阴影部分绕轴旋转所成旋转体的全面积是球的表面积与圆台全面积之和,
解:如图所示,阴影部分绕轴旋转所成旋转体的全面积是球的表面积与圆台全面积之和,
BC=2+4=6,BE=2.
∴CE═4,∴r=2.
S球=4πr2=4π×8=32π,
S圆台=π(22+42+2×6+4×6)=56π,
∴S全=88π.
V=V圆台-V球=
(π•22+π•42+2×4×π)×4-
π×23=
.
 解:如图所示,阴影部分绕轴旋转所成旋转体的全面积是球的表面积与圆台全面积之和,
解:如图所示,阴影部分绕轴旋转所成旋转体的全面积是球的表面积与圆台全面积之和,BC=2+4=6,BE=2.
∴CE═4,∴r=2.
S球=4πr2=4π×8=32π,
S圆台=π(22+42+2×6+4×6)=56π,
∴S全=88π.
V=V圆台-V球=
| 1 |
| 3 |
| 4 |
| 3 |
| 80π |
| 3 |
点评:本题考查旋转体的表面积、体积,组合体的表面积、体积的求法,考查空间想象能力,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图(单位:cm),求图中阴影部分绕AB旋转一周所形成的几何体的表面积和体积.
如图(单位:cm),求图中阴影部分绕AB旋转一周所形成的几何体的表面积和体积.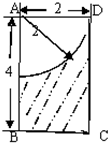 如图,四边形ABCD为矩形,求图中阴影部分绕AB旋转一周所形成的几何体的表面积.
如图,四边形ABCD为矩形,求图中阴影部分绕AB旋转一周所形成的几何体的表面积. 如图所示(单位:cm),四边形ABCD是直角梯形,求图中阴影部分绕AB旋转一周所成几何体的表面积和体积.
如图所示(单位:cm),四边形ABCD是直角梯形,求图中阴影部分绕AB旋转一周所成几何体的表面积和体积. 求图中阴影部分绕轴旋转所成旋转体的全面积和体积.
求图中阴影部分绕轴旋转所成旋转体的全面积和体积.