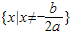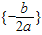题目内容
设一元二次方程ax2+bx+c=0（a＜0）的根的判别式△=b2-4ac=0，则不等式ax2+bx+c≥0的解集为分析：根据根的判别式等于0得到方程有两个相等的实数根，利用求根公式求出方程的根，利用ax2+bx+c=a（x-x1）（x-x2）对不等式变形，然后根据a小于0得到不等式的解集即可．
解答：解：由△=b2-4ac=0可知方程有两个相等的实数根，则方程的根为x1=x2=
=-
，
所以ax2+bx+c≥0变形为a(x+
)2≥0，又a＜0，所以得到(x+
)2=0，解得x=-
，
则不等式ax2+bx+c≥0的解集为{-
}
故答案为{-
}
-b±
| ||
| 2a |
| b |
| 2a |
所以ax2+bx+c≥0变形为a(x+
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
则不等式ax2+bx+c≥0的解集为{-
| b |
| 2a |
故答案为{-
| b |
| 2a |
点评：考查学生会根据求根公式解一元二次方程及会求一元二次不等式的解集．此题的突破点是将不等式进行变形．
练习册系列答案
相关题目
