题目内容
点M、N、P分别是正方体ABCD—A1B1C1D1中的棱CC1、BC、CD的中点.求证:A1P⊥平面DMN.
解析:建立如图所示的空间直角坐标系,设正方体棱长为2,则D(0,0,0),A1(2,0,?2),P(0,1,0),M(0,2,1),N(1,2,0).

∴向量![]() =(0,1,0)-(2,0,2)=(-2,1,-2),
=(0,1,0)-(2,0,2)=(-2,1,-2),
![]() =(0,2,1)-(0,0,0)=(0,2,1),
=(0,2,1)-(0,0,0)=(0,2,1),
DN=(1,2,0).
∴![]() ·
·![]() =(-2,1,-2)·(0,2,1)=(-2)×0+1×2+(-2)×1=0,
=(-2,1,-2)·(0,2,1)=(-2)×0+1×2+(-2)×1=0,
![]() ·
·![]() =(-2,1,-2)·(1,2,0)=(-2)×1+1×2+(-2)×0=0.
=(-2,1,-2)·(1,2,0)=(-2)×1+1×2+(-2)×0=0.
∴![]() ⊥
⊥![]() ,
, ![]() ⊥
⊥![]() ,?
,?
即直线A1P⊥DM,A1P⊥DN.
又∵Dm∩DN=D,∴A1P⊥平面DMN.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
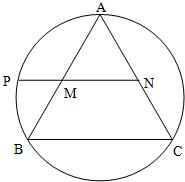 如图,点M,N分别是正△ABC的边AB,AC的中点,直线MN与△ABC的外接圆的一个交点为P.设正△ABC外接圆半径为
如图,点M,N分别是正△ABC的边AB,AC的中点,直线MN与△ABC的外接圆的一个交点为P.设正△ABC外接圆半径为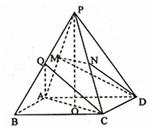 如图,正四棱锥P-ABCD各棱长都为2,点O,M,N,Q分别是AC,PA,PC,PB的中点.
如图,正四棱锥P-ABCD各棱长都为2,点O,M,N,Q分别是AC,PA,PC,PB的中点.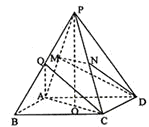
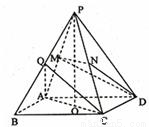 如图,正四棱锥P-ABCD各棱长都为2,点O,M,N,Q分别是AC,PA,PC,PB的中点.
如图,正四棱锥P-ABCD各棱长都为2,点O,M,N,Q分别是AC,PA,PC,PB的中点.