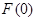题目内容
奇函数y=f(x)在(-∞ ,0)上为减函数,且f(2)=0,则不等式(x-1)f(x-1)>0的解集为
- A.{x|-3<x<-1}
- B.{x|-3<x<1或x>2}
- C.{x|-3<x<0或x>3}
- D.{x|-1<x<1或1<x<3}
D
解:由题意画出f(x)的草图如下,
因为(x-1)f(x-1)>0,所以(x-1)与f(x-1)同号,
由图象可得-2<x-1<0或0<x-1<2,
解得-1<x<1或1<x<3,
故选D.
解:由题意画出f(x)的草图如下,
因为(x-1)f(x-1)>0,所以(x-1)与f(x-1)同号,
由图象可得-2<x-1<0或0<x-1<2,
解得-1<x<1或1<x<3,
故选D.

练习册系列答案
相关题目
对任意的实数a、b ,记 .若
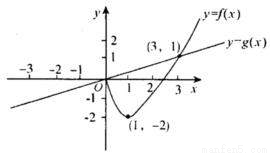
.若 ,其中奇函数y=f(x)在x=l时有极小值-2,y=g(x)是正比例函数,函数
,其中奇函数y=f(x)在x=l时有极小值-2,y=g(x)是正比例函数,函数 与函数y=g(x)的图象如图所示.则下列关于函数
与函数y=g(x)的图象如图所示.则下列关于函数 的说法中,正确的是( )
的说法中,正确的是( )
A. 为奇函数 为奇函数 | B. 的最小值为-2且最大值为2 的最小值为-2且最大值为2 |
C. 在 在 上为增函数 上为增函数 | D. 有极大值 有极大值 且有极小值 且有极小值 |
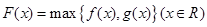 ,其中
,其中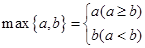
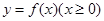 与函数y=g(x)的图象如图所示.则下列关于函数
与函数y=g(x)的图象如图所示.则下列关于函数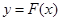 的说法中,正确的是 ( )
的说法中,正确的是 ( )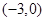 上为增函数
D.
上为增函数
D.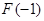 且有极小值
且有极小值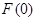
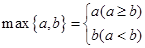 .若
.若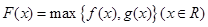 ,其中奇函数y=f(x)在x=l时有极小值-2,y=g(x)是正比例函数,函数
,其中奇函数y=f(x)在x=l时有极小值-2,y=g(x)是正比例函数,函数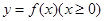 与函数y=g(x)的图象如图所示.则下列关于函数
与函数y=g(x)的图象如图所示.则下列关于函数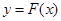 的说法中,正确的是( )
的说法中,正确的是( )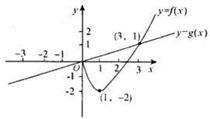
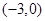 上为增函数 D.
上为增函数 D.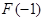 且有极小值
且有极小值