题目内容
已知矩形中ABCD，|AB|=3，|BC|=4，
=
，
=
，
（1）若
=x
+y
，求x，y
（2）求
与
夹角的余弦值．
| e1 |
| ||
|
|
| e2 |
| ||
|
|
（1）若
| AC |
| e1 |
| e2 |
（2）求
| AC |
| BD |
（1）因为矩形中ABCD，|
所以
=
+
，
因为，|AB|=3，|BC|=4，
=
，
=
，
所以
=
+
=3
+ 4
所以x=3，y=4．
（2）因为
=
+
=
-
=4
-3
所以
•
=( 3
+ 4
)•( 4
-3
)=16-9=7|
|
|=|
|=5
设
与
夹角的为θ
所以cosθ=
=
所以
| AC |
| AB |
| BC |
因为，|AB|=3，|BC|=4，
| e1 |
| ||
|
|
| e2 |
| ||
|
|
所以
| AC |
| AB |
| BC |
| e1 |
| e2 |
所以x=3，y=4．
（2）因为
| BD |
| BC |
| CD |
| BC |
| AB |
| e2 |
| e1 |
所以
| AC |
| BD |
| e1 |
| e2 |
| e2 |
| e1 |
|
| AC |
| BD |
设
| AC |
| BD |
所以cosθ=
| ||||
|
|
| 7 |
| 25 |
练习册系列答案
相关题目
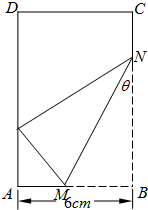已知矩形纸片ABCD中，AB=6cm，AD=12cm，将矩形纸片的右下角折起，使得该角的顶点B落在矩形的边AD上，且折痕MN的端点M，N分别位于边AB，BC上，设∠MNB=θ，sinθ=t，MN长度为l．
，
，
，求x，y
与
夹角的余弦值．
，
，
，求x，y
与
夹角的余弦值．