题目内容
已知椭圆
，的右焦点为F，上顶点为A，P为C1上任一点，圆心在y轴上的圆C2与斜率为
的直线
切于点B
，且AF∥。
（1）求圆的方程及椭圆的离心率。
（2）过P作圆C2的切线PE，PG，若
的最小值为
，求椭圆的方程。
解析(1)由圆心在y轴上的圆C2与斜率为1的直线
切于点B
，所以圆心在过B且垂直于的直线
上，又圆心在y轴上，则圆心C2（0，3），
圆心到直线
的距离
，所以所求圆C2方程为：
，又AF∥，
，所以有
，即
，椭圆的离心率为
；
（2）设
在
中， 
，由椭圆的几何性质有：
，所以有
，因
，所以
，
所以椭圆的方程为
。
练习册系列答案
相关题目
：
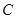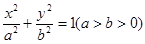的右焦点为F，离心率
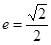，椭圆C上的点到F的距离的最大值为
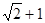，直线l过点F与椭圆C交于不同的两点A、B.
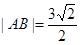，求直线l的方程.
：
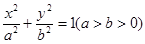的右焦点为F，离心率
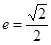，椭圆C上的点到F的距离的最大值为
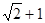，直线l过点F与椭圆C交于不同的两点A、B.
，求直线l的方程.
：
的右焦点为F，离心率
，椭圆C上的点到F的距离的最大值为
，动点
,以OM为直径的圆的圆心是
.
,过N作直径OM的垂线NP,垂足为P,求证：直线NP恒过右焦点F. 
的右焦点为B（1，0），右准线与x轴的交点为A（5，0），过点A作直线
交椭圆C于两个不同的点P、Q．
，若存在，求出