题目内容
（2013•潮州二模）为加强食品安全管理，某市质监局拟招聘专业技术人员x名，行政管理人员y名，若x、y满足
，则z=3x+3y的最大值为（ ）
|
分析：首先作出已知不等式组所对应的平面区域如图，然后设直线l：z=3x+3y，将直线l进行平移，可得当直线l经过交点P（2，2）时，z达到最大值，且x，y都是正整数，从而得到z的最大值．
解答：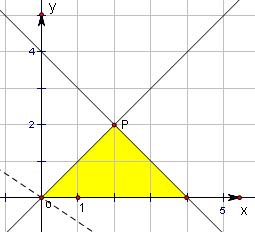
解：将不等式组
，对应的平面区域作出，即图中的三角形及其内部
设直线l：z=3x+3y，将直线l进行平移，当l越向上平移时，z的值越大．
当直线l经过直线y=x与y=-x+4的交点P（2，2）时，z有最大值，且x，y都是正整数
∴z的最大值是2×3+3×2=12
故选B．
解：将不等式组
|
设直线l：z=3x+3y，将直线l进行平移，当l越向上平移时，z的值越大．
当直线l经过直线y=x与y=-x+4的交点P（2，2）时，z有最大值，且x，y都是正整数
∴z的最大值是2×3+3×2=12
故选B．
点评：本题给出目标函数和线性约束条件，要我们求目标函数的最大值，着重考查了简单线性规划及其应用的知识点，属于基础题．
练习册系列答案
相关题目