题目内容
19.在△ABC中,AC=5,$\frac{1}{tan\frac{A}{2}}$+$\frac{1}{tan\frac{C}{2}}$-$\frac{5}{tan\frac{B}{2}}$=0,则BC+AB=( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 作△ABC的内切圆,设O为圆心,r为半径,圆O与三边AB、BC、AC的切点依次为D、E、F,连接OA、OB、OC、OD、OE、OF.则tan$\frac{B}{2}$=$\frac{r}{BD}$,tan$\frac{A}{2}$=$\frac{r}{AF}$,tan$\frac{C}{2}$=$\frac{r}{CF}$,再由已知条件求出AC=5BD,进一步求出BD的值,则BC+AB的答案可求.
解答 解:作△ABC的内切圆,设O为圆心,r为半径,圆O与三边AB、BC、AC的切点依次为D、E、F,连接OA、OB、OC、OD、OE、OF.
则tan$\frac{B}{2}$=$\frac{r}{BD}$,tan$\frac{A}{2}$=$\frac{r}{AF}$,tan$\frac{C}{2}$=$\frac{r}{CF}$.
∵$\frac{1}{tan\frac{A}{2}}$+$\frac{1}{tan\frac{C}{2}}$-$\frac{5}{tan\frac{B}{2}}$=0,
∴$\frac{AF}{r}+\frac{CF}{r}=\frac{5BD}{r}$,
∴AF+CF=5BD,即AC=5BD,
又∵AC=5,
∴BD=1,
∴BE=BD=1,
∴BC+AB=(BE+CE)+(BD+AD)=(CE+AD)+(BE+BD)=AC+2BD=7.
故选:B.
点评 本题考查了三角函数的化简求值,作出△ABC的内切圆是解本题的关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.已知双曲线C的两焦点为F1,F2,离心率为$\frac{4}{3}$,抛物线y2=16x的准线过双曲线C的一个焦点,若以线段F1F2为直径的圆与双曲线交于四个点Pi(i=1,2,3,4),|PiF1|•|PiF2|=( )
| A. | 0 | B. | 7 | C. | 14 | D. | 21 |
20.变量x,y满足约束条件$\left\{\begin{array}{l}x+y≥0\\ x-2y+2≥0\\ mx-y≤0\end{array}\right.$若2x-y的最大值是2,则约束条件表示的平面区域面积为( )
| A. | $\frac{8}{15}$ | B. | $\frac{8}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
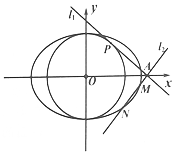 已知椭圆C:$\frac{{x}^{2}}{2}+{y}^{2}=1$和圆O:x2+y2=1,过点A(m,0)(m>1)作两条互相垂直的直线l1,l2,l1于圆O相切于点P,l2与椭圆相交于不同的两点M,N.
已知椭圆C:$\frac{{x}^{2}}{2}+{y}^{2}=1$和圆O:x2+y2=1,过点A(m,0)(m>1)作两条互相垂直的直线l1,l2,l1于圆O相切于点P,l2与椭圆相交于不同的两点M,N.