Question

如图，在直三棱柱ABC-A₁B₁C₁中，E，F分别是AA₁，BC₁的中点．
（Ⅰ）求证：EF∥平面ABC；
（Ⅱ）若AC=

1

2

BC=

2

，AA₁=2，且∠ACB=90°，求平面EBC₁与底面ABC所成的锐二面角的大小．
[注：侧棱垂直于底面的三棱柱叫直三棱柱]．

Answer 1

分析：（I）取BC的中点G，连结AG、FG，利用三角形的中位线定理和平行四边形的性质，证出四边形AEFG是平行四边形，得EF∥AG，再利用线面平行判定定理加以证明，即可得出EF∥平面ABC；
（II）在Rt△A₁EC₁中，利用勾股定理算出C₁E=

3

，同理可得BC₁=2

3

且BE=

11

，利用解三角形知识算出△BC₁E的面积．设平面EBC₁与底面ABC所成的锐二面角为α，算出△ABC的面积，可得cosα=

S△ABC

S△BC1E

=

2

2

，即可得到
平面EBC₁与底面ABC所成的锐二面角的大小．

解答：解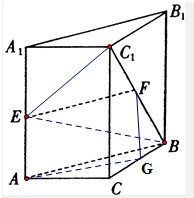：（I）取BC的中点G，连结AG、FG，
∵FG是△BC₁C的中位线，∴FG

∥

.

1

2

C₁C，
∵四边形AA₁C₁C是平行四边形，E为AA₁的中点，
∴AE

∥

.

1

2

C₁C，得FG

∥

.

AE
∴四边形AEFG是平行四边形，得EF∥AG，
∵EF?平面ABC，AG?平面ABC，∴EF∥平面ABC；
（II）∵AA₁⊥平面ABC，AC?平面ABC，∴AA₁⊥A₁C₁，
由此可得Rt△A₁EC₁中，C₁E=

A 1E2+A1C12

=

3

，
同理可得BC₁=

CC12+BC2

=2

3

，
BE=

A  E2+AB2

=

A  E2+AC2+BC2

=

11

，
△BC₁E中，由余弦定理得cos∠BC₁E=

BC12+C1E2-BE2

2×BC1×C1E

=

1

3

，
∴sin∠BC₁E=

1-cos2∠BC1E

=

2 2

3

，
可得S △BC1E=

1

2

BC₁•C₁Esin∠BC₁E=

1

2

×2

3

×

3

×

2 2

3

=2

2

．
∵S_△ABC=

1

2

×AC×BC=

1

2

×

2

×2

2

=2
∴若平面EBC₁与底面ABC所成的锐二面角为α，可得cosα=

S△ABC

S△BC1E

=

2

2

，
由此可得α=45°，即平面EBC₁与底面ABC所成的锐二面角的大小等于45°．

点评：本题在直三棱柱中求证线面平行，并求二面的大小．着重考查了直棱柱的性质、线面平行判定定理、解三角形和二面角的定义与性质等知识，属于中档题．