题目内容
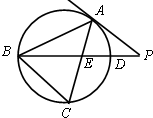
如图，△ABC是⊙O的内接三角形，PA是⊙O的切线，PB交AC于点E，交⊙O于点D．若PA=PE，∠ABC=60°，PD=2，PB=18，则EC=8
8
．分析：利用切割线定理结合题中所给数据，算出PA=6，由弦切角定理结合有一个角为60°的等腰三角形是正三角形，得到PE=AE=6，最后由相交弦定理可得BE•DE=AE•CE，从而求出EC的长．
解答：解：∵PA是圆O的切线，∴PA2=PD•PB=36，可得PA=6
∵∠PAC是弦切角，夹弧ADC，∴∠PAC=∠ABC=60°，
∵△ADE中，PE=PA，∴△APE是正三角形，可得PE=AE=PA=6
∴BE=PB-PE=12，DE=PE-PD=4，
∵圆O中，弦AC、BD相交于E，
∴BE•DE=AE•CE，得12×4=6EC，解之得EC=8
故答案为：8
∵∠PAC是弦切角，夹弧ADC，∴∠PAC=∠ABC=60°，
∵△ADE中，PE=PA，∴△APE是正三角形，可得PE=AE=PA=6
∴BE=PB-PE=12，DE=PE-PD=4，
∵圆O中，弦AC、BD相交于E，
∴BE•DE=AE•CE，得12×4=6EC，解之得EC=8
故答案为：8
点评：本题在圆中给出切线，并且以切线长为一边作正三角形的情况下，求线段的长度．着重考查了切线的性质、正三角形的判定和相交弦定理等知识，属于中档题．
练习册系列答案
相关题目
如图，△ABC是⊙O的内接三角形，PA是⊙O的切线，PB交AC于点E，交⊙O于点D，若PE=PA，∠ABC=60°，PD=1，BD=8，求BC的长．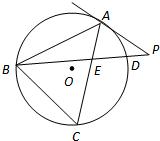
（选修4-1：几何证明选讲）
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分）
[选做题]