题目内容
21、如图，△ABC是⊙O的内接三角形，PA是⊙O的切线，PB交于AC于点E，交⊙O于点D，若PE=PA，∠ABC=60°，PD=1，BD=8，求线段CE的长．
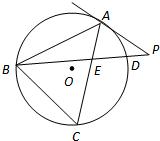
分析：首先根据题中圆的切线条件再依据切割线定理求得一个线段PA的长，再根据线段的关系结合相交弦定理可求得CE的长度即可．
解答：解：∵PA是圆O的切线，PDB是圆O的割线，
∴PA2=PD•PB，又PD=1，BD=8，
∴PA=3，（3分）
又PE=PA，∴PE=3．
∵PA是圆O的切线，
∴∠PAE=∠ABC=60o，
又PE=PA，∴△PAE是等边三角形，
∴PE=3．（7分）
∴DE=PE-PD=2，∴BE=BD-DE=6．
由相交弦定理，得AE•CE=BE•DE，
∴CE=4．（10分）
∴PA2=PD•PB，又PD=1，BD=8，
∴PA=3，（3分）
又PE=PA，∴PE=3．
∵PA是圆O的切线，
∴∠PAE=∠ABC=60o，
又PE=PA，∴△PAE是等边三角形，
∴PE=3．（7分）
∴DE=PE-PD=2，∴BE=BD-DE=6．
由相交弦定理，得AE•CE=BE•DE，
∴CE=4．（10分）
点评：本题考查与圆有关的比例线段、平面几何的切割线定理，属容易题．
练习册系列答案
相关题目
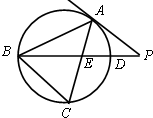如图，△ABC是⊙O的内接三角形，PA是⊙O的切线，PB交AC于点E，交⊙O于点D，若PE=PA，∠ABC=60°，PD=1，BD=8，求BC的长．
（选修4-1：几何证明选讲）
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分）
[选做题]