题目内容
已知二次函数
，其导函数
的图象如图，
（Ⅰ）求函数
处的切线斜率；
（Ⅱ）若函数
上是单调函数，求实数
的取值范围；
（Ⅲ）若
的图像不在函数
图象的下方，求
的取值范围．
解：（1）由已知，
，其图象为直线，且过
两点，
，所以函数
处的切线斜率为0
（2）
|
| （0，1） | 1 | （1，3） | 3 |
|
|
| + | 0 | － | 0 | + |
|
| ↗ | ↘ | ↗ |
的单调递增区间为（0，1）和
的单调递减区间为（1，3）
要使函数
在区间
上是单调函数，则
，解得
（3）由题意，
恒成立，
得
恒成立，
即
恒成立，
设
因为
当
的最小值为
的较小者．
又已知
,
．
练习册系列答案
相关题目
，
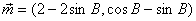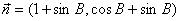，且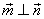
。
)取最大值时，判断三角形ABC的形状。
则
. 
在区间
上有两个零点，则
的取值范围是（ ）
的部分图象如图所示.
的单调递增区间. 
85，乙班学生成绩的平均分为81，则x+y的值为
，若
恒成立，则实数a的取值范围是
(B)
(D)
(B) 
(C)
(D)
为实数，若
，则
”与它的逆命题、否命题、逆否命题这四个命题中，真命题的个数是 ( )