题目内容
(2011•朝阳区三模)若直线l的参数方程为
(t为参数),则直线l的斜率为
)=
,则点A(2,
)到直线m的距离为
.
|
-
| 4 |
| 3 |
-
;在极坐标系中,直线m的方程为ρsin(θ+| 4 |
| 3 |
| π |
| 4 |
| ||
| 2 |
| 7π |
| 4 |
| ||
| 2 |
| ||
| 2 |
分析:①把直线l的参数方程消去参数化为普通方程,得到直线的斜率.②把直线m的极坐标方程消去参数化为普通方程,根据点到直线距离公式计算.
解答:解:①直线l的参数方程为
(t为参数),消去参数t,化为普通方程可得 y=-
(x-1),斜率为 -
.
②直线m的方程为ρsin(θ+
)=
,即
(ρsinθ+ρcosθ)=
,化成普通方程可得x+y=1,即x+y-1=0,
点A(2,
)在平面直角坐标系的坐标为A(
,-
),由点到直线距离公式得A到直线m的距离为 d=
=
故答案为:-
.
|
| 4 |
| 3 |
| 4 |
| 3 |
②直线m的方程为ρsin(θ+
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
点A(2,
| 7π |
| 4 |
| 2 |
| 2 |
| 1 | ||
|
| ||
| 2 |
故答案为:-
| 4 |
| 3 |
| ||
| 2 |
点评:本题考查简单曲线参数方程,普通方程、极坐标方程间的互化,以及点到距离公式的应用.属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2011•朝阳区三模)如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
(2011•朝阳区三模)如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=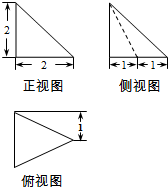 (2011•朝阳区三模)一空间几何体的三视图如图所示,则该几何体的体积为( )
(2011•朝阳区三模)一空间几何体的三视图如图所示,则该几何体的体积为( ) (2011•朝阳区三模)右图是一个几何体的三视图(单位:cm),根据图中数据,可得该几何体的体积是
(2011•朝阳区三模)右图是一个几何体的三视图(单位:cm),根据图中数据,可得该几何体的体积是