题目内容
已知函数f(x)=x2-(a+2)x+alnx,(a∈R)(1)求函数的单调区间与极值点;
(2)若a=4,方程f(x)-m=0有三个不同的根,求m的取值范围.
【答案】分析:(1)对已知函数进行求导,令导数等于0,求出极值点,讨论极值点的大小,利用导数研究函数的单调区间与极值点;
(2)把a=4代入f(x),根据方程f(x)-m=0有三个不同的根,即f(x)=m,有三个解,说明m处在f(x)的最大值和最小值之间,从而进行求解;
解答:解:(1)f′(x)=2x+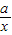 -(a+2)=
-(a+2)=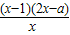 ,
,
令f′(x)=0得x=1或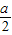 ,
,
当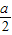 ≤0即a≤0时,x∈(0,1),递增区间为(1,+∞);
≤0即a≤0时,x∈(0,1),递增区间为(1,+∞);
极小值点为1,无极大值点,
当0<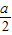 <1即0<a<2时,x∈(0,
<1即0<a<2时,x∈(0,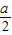 )时,f′(x)>0;
)时,f′(x)>0;
x∈(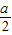 ,1)时,f′(x)<0;
,1)时,f′(x)<0;
x∈(1,+∞)时,f′(x)>0;
∴f(x)的减区间为:(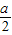 ,1),递增区间为(0,
,1),递增区间为(0,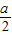 )和(1,+∞);极小值点为1,极大值点为
)和(1,+∞);极小值点为1,极大值点为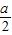 ;
;
当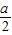 >1即a>2时,x∈(0,1)时,f′(x)>0;
>1即a>2时,x∈(0,1)时,f′(x)>0;
x∈(1,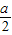 )时,f′(x)<0;
)时,f′(x)<0;
x∈(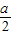 ,+∞)时,f′(x)>0,
,+∞)时,f′(x)>0,
∴f(x)的递减区间为(1,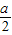 ),递增区间(0,1)和(
),递增区间(0,1)和(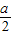 ,+∞);极小值点
,+∞);极小值点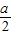 ,极大值点为1;
,极大值点为1;
当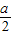 =1时,即a=2时,f′(x)≥0,f(x)在(0,+∞)递增,无减区间,无极值点.
=1时,即a=2时,f′(x)≥0,f(x)在(0,+∞)递增,无减区间,无极值点.
(2)当a=4时,f(x)-m=0即f(x)=m,
由(1)可知,x∈(0,1)时,f(x)递增,x∈(1,2)时,f(x)递减,
x∈(2,+∞)时,f(x)递增;
极大值f(1)=-5,极小值f(2)=4ln2-8,
要使f(x)-m=0有三个不同的根,则4ln2-8<m<-5;
点评:此题主要考查利用导数研究函数的单调性,第一问思路简单,但是讨论情况多比较复杂,第二问就比较简单了,利用数形结合的方法也很容易解决,是一道中档题;
(2)把a=4代入f(x),根据方程f(x)-m=0有三个不同的根,即f(x)=m,有三个解,说明m处在f(x)的最大值和最小值之间,从而进行求解;
解答:解:(1)f′(x)=2x+
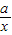 -(a+2)=
-(a+2)=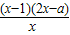 ,
,令f′(x)=0得x=1或
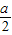 ,
,当
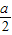 ≤0即a≤0时,x∈(0,1),递增区间为(1,+∞);
≤0即a≤0时,x∈(0,1),递增区间为(1,+∞);极小值点为1,无极大值点,
当0<
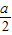 <1即0<a<2时,x∈(0,
<1即0<a<2时,x∈(0,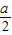 )时,f′(x)>0;
)时,f′(x)>0;x∈(
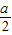 ,1)时,f′(x)<0;
,1)时,f′(x)<0;x∈(1,+∞)时,f′(x)>0;
∴f(x)的减区间为:(
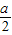 ,1),递增区间为(0,
,1),递增区间为(0,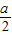 )和(1,+∞);极小值点为1,极大值点为
)和(1,+∞);极小值点为1,极大值点为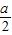 ;
;当
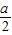 >1即a>2时,x∈(0,1)时,f′(x)>0;
>1即a>2时,x∈(0,1)时,f′(x)>0;x∈(1,
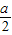 )时,f′(x)<0;
)时,f′(x)<0;x∈(
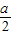 ,+∞)时,f′(x)>0,
,+∞)时,f′(x)>0,∴f(x)的递减区间为(1,
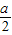 ),递增区间(0,1)和(
),递增区间(0,1)和(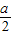 ,+∞);极小值点
,+∞);极小值点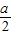 ,极大值点为1;
,极大值点为1;当
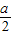 =1时,即a=2时,f′(x)≥0,f(x)在(0,+∞)递增,无减区间,无极值点.
=1时,即a=2时,f′(x)≥0,f(x)在(0,+∞)递增,无减区间,无极值点.(2)当a=4时,f(x)-m=0即f(x)=m,
由(1)可知,x∈(0,1)时,f(x)递增,x∈(1,2)时,f(x)递减,
x∈(2,+∞)时,f(x)递增;
极大值f(1)=-5,极小值f(2)=4ln2-8,
要使f(x)-m=0有三个不同的根,则4ln2-8<m<-5;
点评:此题主要考查利用导数研究函数的单调性,第一问思路简单,但是讨论情况多比较复杂,第二问就比较简单了,利用数形结合的方法也很容易解决,是一道中档题;

练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|