题目内容
设a,b,c都是正数,求证: .
.
证明:∵2( )
)
=( )+(
)+( )+(
)+( )
)
≥2 +2
+2 +2
+2
=2c+2b+2a,
∴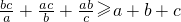
当且仅当a=b=c时,等号成立.
分析:从不等式的左边入手,左边对应的代数式的二倍,分别写成两两相加的形式,在三组相加的式子中分别用均值不等式,整理成最简形式,得到右边的2倍,两边同时除以2,得到结果.
点评:本题考查均值不等式的应用,考查不等式的证明方法,是一个基础题,但是这种题目必须练到过,不然不好考虑,因为题目不符合均值不等式的表现形式.
 )
)=(
 )+(
)+( )+(
)+( )
)≥2
 +2
+2 +2
+2
=2c+2b+2a,
∴
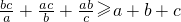
当且仅当a=b=c时,等号成立.
分析:从不等式的左边入手,左边对应的代数式的二倍,分别写成两两相加的形式,在三组相加的式子中分别用均值不等式,整理成最简形式,得到右边的2倍,两边同时除以2,得到结果.
点评:本题考查均值不等式的应用,考查不等式的证明方法,是一个基础题,但是这种题目必须练到过,不然不好考虑,因为题目不符合均值不等式的表现形式.

练习册系列答案
相关题目
设a,b,c都是正数,且3a=4b=6c,那么( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|