Question

不论m为何实数，直线(m－1)x－y＋2m＋1＝0 恒过定点                      （   ）

A．(1, 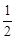－)         B．(－2, 0)           C．(2, 3)             D．(－2, 3)

 

Answer 1

【答案】

D

【解析】

试题分析：将直线的方程（m-1）x-y+2m+1=0是过某两直线交点的直线系，故其一定通过某个定点，将其整理成直线系的标准形式，求两定直线的交点此点即为直线恒过的定点。

因为不论m为何实数，直线(m－1)x－y＋2m＋1＝0 恒过定点，则可知m(2+x)-x-y+1=0,恒成立，则说明m的系数为零，即x+2=0,x+y-1=0,解方程组可知交点的坐标为.(－2, 3)，故选D.

考点：直线方程的运用。

点评：本试题考查了过两直线相交的交点的直线系的设法，进而求解直线方程，属于基础题。