题目内容
10、三次函数y=ax3+x在（-∞，+∞）内单调递增，则实数a的取值范围是
a＞0
．分析：求出函数f（x）的导函数，令导函数大于等于0在（-∞，+∞）上恒成立，令二次项的系数大于0即可．
解答：解：∵f′（x）=3ax2+1
又三次函数y=ax3+x在（-∞，+∞）内单调递增
∴f′（x）=3ax2+1≥0在（-∞，+∞）恒成立
∴a＞0
故答案为：a＞0．
又三次函数y=ax3+x在（-∞，+∞）内单调递增
∴f′（x）=3ax2+1≥0在（-∞，+∞）恒成立
∴a＞0
故答案为：a＞0．
点评：解决函数的单调性已知求参数范围问题，常求出导函数，令导函数大于等于（或小于等于）0恒成立．
练习册系列答案
相关题目
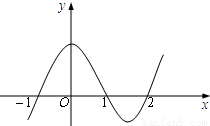
如图，三次函数y=ax3+bx2+cx+d的零点为-1，1，2，则该函数的单调减区间为