题目内容
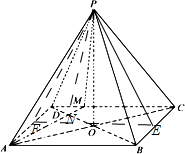
 如图,四棱锥P-ABCD中,PA=PB=PC=PD=1,∠APB=∠DPC=90°,∠BPC=∠APD=60°.
如图,四棱锥P-ABCD中,PA=PB=PC=PD=1,∠APB=∠DPC=90°,∠BPC=∠APD=60°.(Ⅰ)求证:底面ABCD为矩形;
(Ⅱ)在DC取一点M,使得PB⊥平面PAM,求直线PA与平面PBD所成角的正弦值.
考点:直线与平面所成的角,平面的基本性质及推论,点、线、面间的距离计算
专题:计算题,证明题,空间位置关系与距离,空间角
分析:(Ⅰ)由条件得到△PAB≌△PDC,△PBC≌△PAD,从而得AB=DC,BC=AD,即底面ABCD为平行四边形,取BC,AD的中点分别为E,F,证得BC⊥平面PEF,从而AB⊥BC,结论成立;
(Ⅱ)首先证得AM⊥平面PBD,从而∠APN为直线PA与平面PBD所成的角,通过解△ABD,求出AN,sin∠APN,即可得到答案.
(Ⅱ)首先证得AM⊥平面PBD,从而∠APN为直线PA与平面PBD所成的角,通过解△ABD,求出AN,sin∠APN,即可得到答案.
解答:
 (Ⅰ)证明∵PA=PB=PC=PD=1,∠APB=∠DPC=90°,∠BPC=∠APD=60°,
(Ⅰ)证明∵PA=PB=PC=PD=1,∠APB=∠DPC=90°,∠BPC=∠APD=60°,
∴△PAB≌△PDC,△PBC≌△PAD,
∴AB=DC,BC=AD,
∴底面ABCD为平行四边形,
取BC,AD的中点分别为E,F,则BC⊥PE,AD⊥PF,又BC∥AD,
∴BC⊥PF,∴BC⊥平面PEF,BC⊥EF,
显然AB∥EF,∴AB⊥BC,∴底面ABCD为矩形;
(Ⅱ)解:连接AC,BD交于点O,则PO⊥底面ABCD,
∵PB⊥平面PAM,∴PB⊥AM,
又AM⊥PO,∴AM⊥平面PBD,
设AM∩平面PBD=N,
∴∠APN为直线PA与平面PBD所成的角.
在△ABD中,AN=
=
,
sin∠APN=
=
.
∴直线PA与平面PBD所成的角的正弦值为
.
 (Ⅰ)证明∵PA=PB=PC=PD=1,∠APB=∠DPC=90°,∠BPC=∠APD=60°,
(Ⅰ)证明∵PA=PB=PC=PD=1,∠APB=∠DPC=90°,∠BPC=∠APD=60°,∴△PAB≌△PDC,△PBC≌△PAD,
∴AB=DC,BC=AD,
∴底面ABCD为平行四边形,
取BC,AD的中点分别为E,F,则BC⊥PE,AD⊥PF,又BC∥AD,
∴BC⊥PF,∴BC⊥平面PEF,BC⊥EF,
显然AB∥EF,∴AB⊥BC,∴底面ABCD为矩形;
(Ⅱ)解:连接AC,BD交于点O,则PO⊥底面ABCD,
∵PB⊥平面PAM,∴PB⊥AM,
又AM⊥PO,∴AM⊥平面PBD,
设AM∩平面PBD=N,
∴∠APN为直线PA与平面PBD所成的角.
在△ABD中,AN=
| AB•AD |
| BD |
| ||
|
sin∠APN=
| AN |
| AP |
| ||
| 3 |
∴直线PA与平面PBD所成的角的正弦值为
| ||
| 3 |
点评:本题考查空间直线与平面垂直的判定和性质,考查直线与平面所成的角的大小,考查基本的运算能力,属于基础题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目




 如图1,等腰梯形ABCD中,AD∥BC,AD=
如图1,等腰梯形ABCD中,AD∥BC,AD= 如图所示,已知四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,∠BAD
如图所示,已知四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD为直角梯形,∠BAD 某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表:
某数学老师对本校2013届高三学生的高考数学成绩按1:200进行分层抽样抽取了20名学生的成绩,并用茎叶图记录分数如图所示,但部分数据不小心丢失,同时得到如下所示的频率分布表: