题目内容
已知函数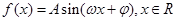 (其中
(其中 )的图象与x轴的相邻两个交点之间的距离为
)的图象与x轴的相邻两个交点之间的距离为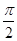 ,且图象上一个最高点为
,且图象上一个最高点为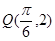
(1)求 的解析式;
的解析式;
(2)当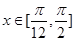 ,求
,求 的值域.
的值域.
(1) (2)[-1,2]
(2)[-1,2]
解析试题分析:(1)求三角函数解析式,基本方法为待定系数法,就是确定 值. 由最高点为
值. 由最高点为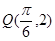 得A="2." 由x轴上相邻的两个交点之间的距离为
得A="2." 由x轴上相邻的两个交点之间的距离为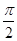 得
得 =
=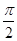 ,即
,即 ,
, ,由
,由 得
得 ,又
,又
(2)对基本三角函数研究性质,可结合图像进行列式. 因为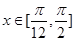 ,所以当
,所以当 =
=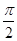 ,即
,即 时,
时, 取得最大值2;当
取得最大值2;当 即
即 时,
时, 取得最小值-1,故
取得最小值-1,故 的值域为[-1,2]
的值域为[-1,2]
试题解析:(1)由最高点为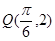 得A=2.
得A=2.
由x轴上相邻的两个交点之间的距离为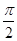 得
得 =
=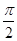 ,即
,即 ,
,
由点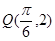 在图像上得
在图像上得

故


又
(2)

当 =
=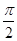 ,即
,即 时,
时, 取得最大值2;当
取得最大值2;当
即 时,
时, 取得最小值-1,故
取得最小值-1,故 的值域为[-1,2]
的值域为[-1,2]
考点:三角函数解析式,三角函数性质

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
 .
.
 的最小正周期;
的最小正周期;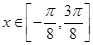 时,求函数f(x)的单调区间。
时,求函数f(x)的单调区间。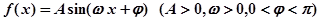 的部分图象,如图所示.
的部分图象,如图所示.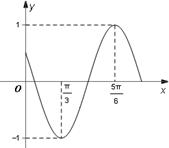
 在
在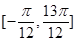 有两个不同的实根,求
有两个不同的实根,求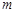 的取值范围.
的取值范围.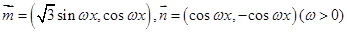 ,函数
,函数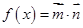 的最小正周期为
的最小正周期为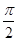 .
.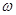 的值;
的值;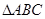 的三边
的三边 、
、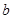 、
、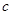 满足:
满足: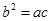 ,且边
,且边 ,若关于
,若关于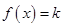 有两个不同的实数解,求实数
有两个不同的实数解,求实数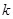 的取值范围.
的取值范围.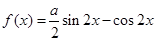 的图象过点
的图象过点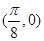 .
.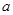 的值;
的值; 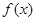 的最小正周期及最大值.
的最小正周期及最大值. =
= ,那么sin
,那么sin 的值为 ,cos2
的值为 ,cos2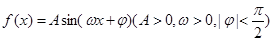 的部分图象如图所示。
的部分图象如图所示。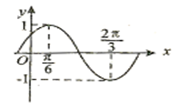
 的最小正周期及解析式;
的最小正周期及解析式;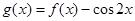 ,求函数
,求函数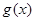 在区间
在区间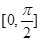 上的最小值.
上的最小值. cos4x
cos4x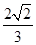 ,f(
,f(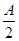 )=-
)=-