题目内容
数列{bn}的通项公式bn=2n-49,则{bn}的前n项和取得最小值时,n等于______.
∵数列{bn}的bn=2n-49,
∴数列{bn}为等差数列,
且b1=-47,b2=-45.∴d=2,sn=nb1+
=-47n+n(n-1)=n2-48n
当n=24时sn取得最小值.
故答案为24
∴数列{bn}为等差数列,
且b1=-47,b2=-45.∴d=2,sn=nb1+
| n(n-1)d |
| 2 |
当n=24时sn取得最小值.
故答案为24

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
 ,Tn为数列{bn}的前n项和,求Tn.
,Tn为数列{bn}的前n项和,求Tn.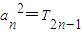 ,求通项an;
,求通项an;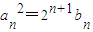 .
.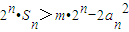 对?n∈N*恒成立,求m的取值范围.
对?n∈N*恒成立,求m的取值范围.