题目内容
在 中,角
中,角 为锐角,已知内角
为锐角,已知内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,向量
,向量 且向量
且向量 共线.
共线.
(1)求角 的大小;
的大小;
(2)如果 ,且
,且 ,求
,求 .
.
 中,角
中,角 为锐角,已知内角
为锐角,已知内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,向量
,向量 且向量
且向量 共线.
共线.(1)求角
 的大小;
的大小;(2)如果
 ,且
,且 ,求
,求 .
.(1) ,(2)
,(2)
 ,(2)
,(2)
试题分析:(1)由向量共线关系得到一个等量关系:
 利用二倍角公式化简得:
利用二倍角公式化简得: ,又
,又 ,所以
,所以 =
= ,即
,即 (2)结合(1),本题就是已知角B,所以三角形面积公式选用含B角,即
(2)结合(1),本题就是已知角B,所以三角形面积公式选用含B角,即 ,所以
,所以 ,再结合余弦定理得:
,再结合余弦定理得:
 ,
, .应用余弦定理时,要注意代数变形,即
.应用余弦定理时,要注意代数变形,即 ,这样只需整体求解即可.
,这样只需整体求解即可.试题解析:(1)由向量
 共线有:
共线有: 
即
 , 5分
, 5分又
 ,所以
,所以 ,则
,则 =
= ,即
,即 8分
8分(2)由
 ,得
,得 10分
10分由余弦定理得

得
 15分
15分故
 16分
16分
练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 中,已知向量
中,已知向量 ,
, ,且
,且 。
。
 与
与 间的关系;(2)若
间的关系;(2)若 ,求
,求 的面积.
的面积. ,
, 是平面内两个不共线的向量,
是平面内两个不共线的向量, =(a﹣1)
=(a﹣1) ,
, =b
=b ﹣2
﹣2 +
+ 的最小值是( )
的最小值是( ) ,
, ,
, ,那么
,那么 为( )
为( )



 ,
, ,且
,且
 ,则锐角
,则锐角 为______________.
为______________. 共线的单位向量是
共线的单位向量是 ;
; 的最小正周期为
的最小正周期为 ;
; 是偶函数;
是偶函数; 是
是 所在平面内一点,若
所在平面内一点,若 ,则
,则 的值域为
的值域为 ,则
,则 的取值范围是
的取值范围是 .
.
 -
- =
=
 =
=
 +
+ +
+ =
= +
+
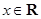 ,向量
,向量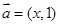 ,
,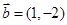 ,且
,且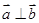 ,则
,则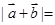 .
. ,
, 若
若 ,则
,则 _____________.
_____________.