Question

已知函数y=cos²x+sinxcosx+1,x∈R.

(1)求它的振幅、周期和初相；

(2)用五点法作出它的简图；

(3)该函数的图象是由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到的？

Answer 1

解：y=cos²x+sinxcosx+1=cos2x+sin2x+

=sin(2x+)+.

(1)y=cos²x+sinxcosx+1的振幅为A=，周期为T==π，初相为φ=.

(2)令x₁=2x+，则y=sin(2x+)+=sinx₁+，列出下表，并描出如下图象：

x
x1	0		π		2π
y=sinx1	0	1	0	-1	0
y=sin(2x+)+

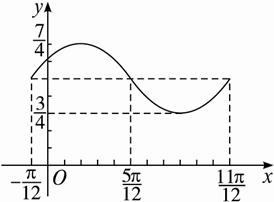
(3)解法一：将函数图象依次作如下变换：

函数y=sinx的图象函数y=sin(x+)的图象

函数y=sin(2x+)的图象

函数y=sin(2x+)的图象

函数y=sin(2x+)+的图象.

即得函数y=cos²x+sinxcosx+1的图象.

解法二：函数y=sinx的图象

函数y=sin2x的图象函数y=sin(2x+)的图象

函数y=sin(2x+)+的图象

函数y=sin(2x+)+的图象.

即得函数y=cos²x+sinxcosx+1的图象.