题目内容
设函数 ,
,
(Ⅰ)求f(x)的单调区间和极值;
(Ⅱ)若对一切x∈R,-3≤af(x)+b≤3,求a-b的最大值。
 ,
,(Ⅰ)求f(x)的单调区间和极值;
(Ⅱ)若对一切x∈R,-3≤af(x)+b≤3,求a-b的最大值。
解:(Ⅰ) ,
,
当x∈(-2,1)时,f′(x)>0;当x∈ 或x∈
或x∈ 时,f′(x)<0;
时,f′(x)<0;
故f(x)在(-2,1)上单调增加,在 ,
, 上单调减少,
上单调减少,
∴f(x)的极小值 ,极大值f(1)=1;
,极大值f(1)=1;
(Ⅱ)由 知
知 ,
,
即 ,
,
由此及(Ⅰ)知f(x)的最小值为 ,最大值为1,
,最大值为1,
因此对一切x∈R,-3≤af(x)+b≤3的充要条件是 ,
,
即a,b满足约束条件 ,
,
由线性规划得,a-b的最大值为5.
 ,
,当x∈(-2,1)时,f′(x)>0;当x∈
 或x∈
或x∈ 时,f′(x)<0;
时,f′(x)<0;故f(x)在(-2,1)上单调增加,在
 ,
, 上单调减少,
上单调减少,∴f(x)的极小值
 ,极大值f(1)=1;
,极大值f(1)=1;(Ⅱ)由
 知
知 ,
,即
 ,
,由此及(Ⅰ)知f(x)的最小值为
 ,最大值为1,
,最大值为1,因此对一切x∈R,-3≤af(x)+b≤3的充要条件是
 ,
,即a,b满足约束条件
 ,
,由线性规划得,a-b的最大值为5.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
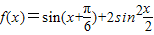 .
.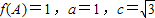 ,求b值.
,求b值.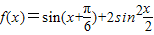 .
. ,求b值.
,求b值. .
. ,求
,求 的值.
的值. .
.
 时,求sin2x.
时,求sin2x.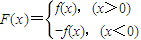 .
.