题目内容
已知抛物线的焦点F在y轴上,抛物线上一点A(a,4)到准线的距离是5,过点F的直线与抛物线交于M、N两点,过M、N两点分别作抛物线的切线,这两条切线的交点为T,
(Ⅰ)求抛物线的标准方程;
(Ⅱ)求 的值;
的值;
( Ⅲ)求证: 是
是 和
和 的等比中项。
的等比中项。
(Ⅰ)求抛物线的标准方程;
(Ⅱ)求
 的值;
的值;( Ⅲ)求证:
 是
是 和
和 的等比中项。
的等比中项。(Ⅰ)解:由题意可设抛物线的方程为x2=2py(p≠0),
因为点A(a,4)在抛物线上,所以p>0,
又点A(a,4)到抛物线准线的距离是5,
所以, +4=5,可得p=2,
+4=5,可得p=2,
所以抛物线的标准方程为x2=4y。
(Ⅱ)解:点F为抛物线的焦点,则F(0,1),
依题意可知直线MN不与x轴垂直,
所以设直线MN的方程为y=kx+1,
因为MN过焦点F,所以判别式大于0,
设M(x1,y1),N(x2,y2),
则x1+x2=4k,x1x2=-4,
 ,
,
由于 ,所以,
,所以, ,
,
切线MT的方程为 , ①
, ①
切线NT的方程为 , ②
, ②
由①,②得 ,
,
则 ,
,
所以, 。
。
(Ⅲ)证明: ,
,
由抛物线的定义,知 ,
,
则
 ,
,
所以, ,
,
即 是
是 和
和 的等比中项。
的等比中项。
因为点A(a,4)在抛物线上,所以p>0,
又点A(a,4)到抛物线准线的距离是5,
所以,
 +4=5,可得p=2,
+4=5,可得p=2,所以抛物线的标准方程为x2=4y。
(Ⅱ)解:点F为抛物线的焦点,则F(0,1),
依题意可知直线MN不与x轴垂直,
所以设直线MN的方程为y=kx+1,
因为MN过焦点F,所以判别式大于0,
设M(x1,y1),N(x2,y2),
则x1+x2=4k,x1x2=-4,
 ,
,由于
 ,所以,
,所以, ,
,切线MT的方程为
 , ①
, ①切线NT的方程为
 , ②
, ②由①,②得
 ,
,则
 ,
,所以,
 。
。(Ⅲ)证明:
 ,
,由抛物线的定义,知
 ,
,则

 ,
,所以,
 ,
,即
 是
是 和
和 的等比中项。
的等比中项。
练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
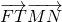 的值;
的值;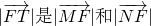 的等比中项.
的等比中项.