题目内容
已知函数 在
在 上恒为正,则实数a的取值范围 .
上恒为正,则实数a的取值范围 .
【答案】分析:讨论a与1的大小,将函数f(x)=loga(ax2-x+ )(a>0且a≠1)在[
)(a>0且a≠1)在[ ,2]上恒正转化成:当0<a<1时,0<ax2-x+
,2]上恒正转化成:当0<a<1时,0<ax2-x+ <1在[
<1在[ ,2]上恒成立,当a>1时,ax2-x+
,2]上恒成立,当a>1时,ax2-x+ >1在[
>1在[ ,2]上恒成立,然后利用分离法可求出a的取值范围.
,2]上恒成立,然后利用分离法可求出a的取值范围.
解答:解:当0<a<1时,
若函数f(x)=loga(ax2-x+ )(a>0且a≠1)在[
)(a>0且a≠1)在[ ,2]上恒正
,2]上恒正
即0<ax2-x+ <1在[
<1在[ ,2]上恒成立,
,2]上恒成立,
∴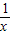 -
-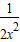 <a<
<a<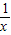 +
+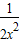
而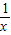 -
-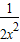 在[
在[ ,2]上的最大值为
,2]上的最大值为 ,
,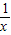 +
+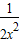 在[
在[ ,2]上的最小值为
,2]上的最小值为
∴此时 <a<
<a<
当a>1时,函数f(x)=loga(ax2-x+ )(a>0且a≠1)在[
)(a>0且a≠1)在[ ,2]上恒正
,2]上恒正
则ax2-x+ >1在[
>1在[ ,2]上恒成立,
,2]上恒成立,
即a>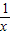 +
+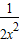 在[
在[ ,2]上恒成立
,2]上恒成立
而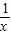 +
+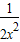 在[
在[ ,2]上的最大值为4
,2]上的最大值为4
∴此时a>4
故答案为:( ,
, )∪(4,+∞)
)∪(4,+∞)
点评:本题主要考查了函数恒成立问题,同时考查了分类讨论、转化的思想和运算求解的能力,属于中档题.
 )(a>0且a≠1)在[
)(a>0且a≠1)在[ ,2]上恒正转化成:当0<a<1时,0<ax2-x+
,2]上恒正转化成:当0<a<1时,0<ax2-x+ <1在[
<1在[ ,2]上恒成立,当a>1时,ax2-x+
,2]上恒成立,当a>1时,ax2-x+ >1在[
>1在[ ,2]上恒成立,然后利用分离法可求出a的取值范围.
,2]上恒成立,然后利用分离法可求出a的取值范围.解答:解:当0<a<1时,
若函数f(x)=loga(ax2-x+
 )(a>0且a≠1)在[
)(a>0且a≠1)在[ ,2]上恒正
,2]上恒正即0<ax2-x+
 <1在[
<1在[ ,2]上恒成立,
,2]上恒成立,∴
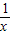 -
-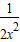 <a<
<a<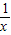 +
+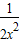
而
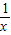 -
-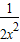 在[
在[ ,2]上的最大值为
,2]上的最大值为 ,
,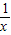 +
+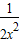 在[
在[ ,2]上的最小值为
,2]上的最小值为
∴此时
 <a<
<a<
当a>1时,函数f(x)=loga(ax2-x+
 )(a>0且a≠1)在[
)(a>0且a≠1)在[ ,2]上恒正
,2]上恒正则ax2-x+
 >1在[
>1在[ ,2]上恒成立,
,2]上恒成立,即a>
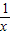 +
+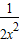 在[
在[ ,2]上恒成立
,2]上恒成立而
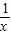 +
+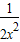 在[
在[ ,2]上的最大值为4
,2]上的最大值为4∴此时a>4
故答案为:(
 ,
, )∪(4,+∞)
)∪(4,+∞)点评:本题主要考查了函数恒成立问题,同时考查了分类讨论、转化的思想和运算求解的能力,属于中档题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
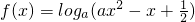 在
在 上恒为正,则实数a的取值范围________.
上恒为正,则实数a的取值范围________. 在
在 上恒为正,则实数a的取值范围 .
上恒为正,则实数a的取值范围 .