题目内容
已知函数![]() ,其中
,其中![]()
![]() .
.
(Ⅰ)求证:![]() 是
是![]() 是奇函数的充要条件;
是奇函数的充要条件;
(Ⅱ)若常数n=-4且![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
解:(I)充分性:若![]() ,则
,则![]() , ∴
, ∴![]() ,
,
又有![]() ,∴
,∴![]() 为奇函数.
为奇函数.
必要性:若![]() 为奇函数,∵
为奇函数,∵![]() ,
,
∴![]() ,即
,即![]() ,∴
,∴![]() .
.
由![]() ,有
,有![]() ,∴
,∴![]() .
.
∴ ![]() 为奇函数,则
为奇函数,则![]() ,即
,即![]() .
.
∴![]() 是
是![]() 为奇函数的充要条件.
为奇函数的充要条件.
(Ⅱ)若![]() 时,
时,![]() 恒成立;
恒成立;
若![]() 时,原不等式可变形为
时,原不等式可变形为![]() . 即
. 即![]() .
.
|

对①式![]() 在
在![]() 上单调递减.
上单调递减.
∴![]() . ③
. ③
对②式,设![]() ,根据单调函数的定义可证明
,根据单调函数的定义可证明![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() .
.
∴![]() . ④
. ④
由③④知![]() .
.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目






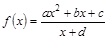 (其中
(其中 是实数常数,
是实数常数, )
) ,函数
,函数 的图像关于点(—1,3)成中心对称,求
的图像关于点(—1,3)成中心对称,求 的值;
的值; ,总有
,总有 ,求
,求 的取值范围;
的取值范围; ,
, ,且对任意
,且对任意 时,不等式
时,不等式 恒成立,求负实数
恒成立,求负实数 的取值范围.
的取值范围.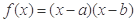 (其中
(其中 )的图象如图(上)所示,则函数
)的图象如图(上)所示,则函数 的图象是( )
的图象是( ) 
