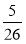Question

在四面体ABCD中，有如下结论：

①若，则；

②若分别是的中点，则的大小等于异面直线与所成角的大小；

③若点是四面体外接球的球心，则在面上的射影为的外心；

④若四个面是全等的三角形，则为正四面体.

其中所有正确结论的序号是 .

 

Answer 1

①③

【解析】

试题分析：对于①，如图（1），作面，则有，而，所以面，所以，同理可证，故为三角形的垂心，所以，而，所以平面，故，命题正确；对于②，应该讲当为锐角或直角时，等于异面直线与所成的角，当为钝角时，的补角才等于异面直线与所成的角，命题不正确；对于③，根据球的性质：球心与小圆圆心（本题中相当于外接圆的圆心）相连垂直于小圆所在的平面，可知该命题正确；对于④，如下图（2），其中，易知该三棱锥的四个面都是全等的三角形，但该三棱锥并不是正四面体.

考点：1.空间中的垂直问题；2.异面直线成角的理解；3.球的性质；4.正四面体的结构.