Question

已知函数f（x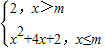）=的图象与直线y=x恰有三个公共点，则实数m的取值范围是（ ）
A．（-∞，-1]
B．[-1，2）
C．[-1，2]
D．[2，+∞）

Answer 1

【答案】分析：由题意可得只要满足直线y=x和射线y=2（x＞m）有一个交点，而且直线y=x与函数f（x）=x²+4x+2的两个交点即可，画图便知，直线y=x与函数f（x）=x²+4x+2的图象的
两个交点为（-2，-2）（-1，-1），由此可得实数m的取值范围．
解答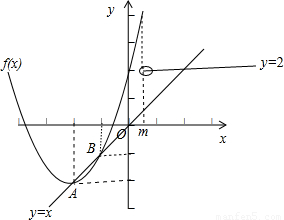：解：由题意可得射线y=x与函数f（x）=2（x＞m）有且只有一个交点．
而直线y=x与函数f（x）=x²+4x+2，至多两个交点，
题目需要三个交点，则只要满足直线y=x与函数f（x）=x²+4x+2的图象有两个交点即可，
画图便知，y=x与函数f（x）=x²+4x+2的图象交点为A（-2，-2）、B（-1，-1），故有 m≥-1．
而当m≥2时，直线y=x和射线y=2（x＞m）无交点，故实数m的取值范围是[-1，2），
故选B．
点评：本题主要考查函数与方程的综合应用，体现了转化、数形结合的数学思想，属于基础题．