题目内容
20.设行列式$|\begin{array}{l}{{a}_{11}}&{{a}_{12}}\\{{a}_{21}}&{{a}_{22}}\end{array}|=m,|\begin{array}{l}{{a}_{13}}&{{a}_{11}}\\{{a}_{23}}&{{a}_{21}}\end{array}|$=n,则行列式$|\begin{array}{l}{{a}_{11}}&{{a}_{12}+{a}_{13}}\\{{a}_{21}}&{{a}_{22}+{a}_{23}}\end{array}|$等于( )| A. | m+n | B. | -(m+n) | C. | n-m | D. | m-n |
分析 利用二阶行列式展开法则进行求解.
解答 解:∵$|\begin{array}{l}{{a}_{11}}&{{a}_{12}}\\{{a}_{21}}&{{a}_{22}}\end{array}|=m,|\begin{array}{l}{{a}_{13}}&{{a}_{11}}\\{{a}_{23}}&{{a}_{21}}\end{array}|$=n,
∴m=a11a22-a21a12,
n=a13a21-a23a11,
∴$|\begin{array}{l}{{a}_{11}}&{{a}_{12}+{a}_{13}}\\{{a}_{21}}&{{a}_{22}+{a}_{23}}\end{array}|$=a11(a22+a23)-a21(a12+a13)
=a11a22-a21a12-(a21a13-a23a11)
=m-n.
故选:D.
点评 本题考查二阶行列式的计算,是基础题,解题时要注意二阶行列式展开法则的合理运用.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
10.函数f(x)=2-|x+1|的单调递增区间为( )
| A. | (-∞,-1) | B. | (-∞,0) | C. | (0,+∞) | D. | (-1,+∞) |
11.上饶某中学研究性学习小组为调查市民喜欢观看体育节目是否与性别有关,随机抽取了55名市民,得到数据如下表:
(1)判断是否有99.5%的把握认为喜欢观看体育节目与性别有关?
(2)用分层抽样的方法从喜欢观看体育节目的市民中随机抽取6人作进一步调查,将这6位市民作为一个样本,从中任选2人,求男市民人数ξ的分布列和期望.
下面的临界值表参考:
| 喜欢 | 不喜欢 | 合计 | |
| 男 | 20 | 5 | 25 |
| 女 | 10 | 20 | 30 |
| 合计 | 30 | 25 | 55 |
(2)用分层抽样的方法从喜欢观看体育节目的市民中随机抽取6人作进一步调查,将这6位市民作为一个样本,从中任选2人,求男市民人数ξ的分布列和期望.
下面的临界值表参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
8.已知函数f(x)=loga(x2+1)(a>0)在[0,1]上的最大值为1,函数g(x)=($\frac{1}{3}$)x-m,若?x1∈[0,3],?x2∈[1,2],使得f(x1)≥g(x2),则实数m的取值范围是( )
| A. | [$\frac{1}{9}$,+∞) | B. | [$\frac{1}{3}$,+∞) | C. | (-∞,$\frac{1}{9}$] | D. | (-∞,$\frac{1}{3}$] |
5.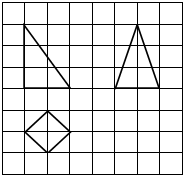 如图,网格纸上小正方形的边长为1,粗实线画出的是某底面为正方形的四棱锥的三视图,则该四棱锥的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某底面为正方形的四棱锥的三视图,则该四棱锥的表面积为( )
 如图,网格纸上小正方形的边长为1,粗实线画出的是某底面为正方形的四棱锥的三视图,则该四棱锥的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某底面为正方形的四棱锥的三视图,则该四棱锥的表面积为( )| A. | $\sqrt{2}$+$\sqrt{6}$ | B. | 2+2$\sqrt{6}$ | C. | 2+2$\sqrt{2}$+2$\sqrt{6}$ | D. | 2+3$\sqrt{2}$+$\sqrt{22}$ |
