题目内容
已知函数
(1)当 时,求函数
时,求函数 在
在 上的极值;
上的极值;
(2)证明:当 时,
时, ;
;
(3)证明:
 .
.
解 (1)当

 变化如下表
变化如下表
|
|
|
|
|
|
|
|
| + | 0 | - | 0 | + |
|
| ↗ | 极大值 | ↘ | 极小值 | ↗ |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在 中,
中,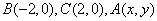 ,给出
,给出 满足的条件,就能得到动点
满足的条件,就能得到动点
的轨迹方程,下表给出了一些条件及方程:
| 条件 | 方程 |
| ① |
|
| ② |
|
| ③ |
|
则满足条件①、②、③的点 轨迹方程按顺序分别是
轨迹方程按顺序分别是
A. 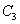 、
、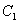 、
、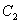 B.
B. 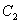 、
、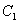 、
、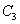
C. 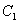 、
、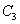 、
、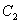 D.
D. 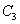 、
、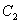 、
、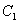




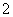



 则
则 .
. .
. 种(用数字作答).
种(用数字作答). 框格内有一块花纹(如图所示),花纹刚好过点
框格内有一块花纹(如图所示),花纹刚好过点 ,经研究发现花纹边界是函数
,经研究发现花纹边界是函数 与
与 图象的一部分,现任取一个点
图象的一部分,现任取一个点 ,则点
,则点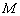 取自阴影部分的概率为 . .
取自阴影部分的概率为 . .



 与平面
与平面 ,给出下列三个结论:①若
,给出下列三个结论:①若 ∥
∥ ,
, ∥
∥ ,则
,则 ; ③若
; ③若 ,
, ,则
,则 .
.