题目内容
已知函数
(1)求函数f(x)的单调区间;
(2)解不等式 .
.
(3)若不等式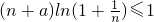 对任意n∈N*都成立,求a的最大值.
对任意n∈N*都成立,求a的最大值.
解:(1) ,定义域{x|x>0}.
,定义域{x|x>0}.
∵ ,
,
∴f(x)在(0,+∞)上是减函数.
(2)对 当x≥1时,原不等式变为
当x≥1时,原不等式变为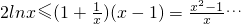 ①
①
由(1)结论,x≥1时,f(x)≤f(1)=0, 即①成立
即①成立
当0<x≤1时,原不等式变为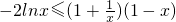 ,
,
即 ②
②
由(1)结论0<x≤1时,f(x)≥f(1)=0, 即②成立
即②成立
综上得,所求不等式的解集是{x|x>0}
(3)结论:a的最大值为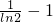 .
.
证明:∵n∈N*,
∴ ,
,
∵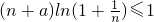 ,
,
∴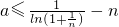 ,取
,取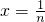 ,则x∈(0,1],
,则x∈(0,1],
∴ ,
,
设 ,
,
则 ,∴g(x)在x∈(0,1]上单调递减,
,∴g(x)在x∈(0,1]上单调递减,
∴当x=1时, .
.
∴a的最大值为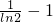 .
.
分析:(1)利用导数即可求出其单调区间;
(2)通过对x讨论,再利用(1)的结论即可;
(3)通过分离参数,通过换元求导,再利用(1)的结论即可得出.
点评:熟练掌握利用导数研究函数的单调性、分离参数法和换元法是解题的关键.
 ,定义域{x|x>0}.
,定义域{x|x>0}.∵
 ,
,∴f(x)在(0,+∞)上是减函数.
(2)对
 当x≥1时,原不等式变为
当x≥1时,原不等式变为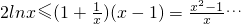 ①
①由(1)结论,x≥1时,f(x)≤f(1)=0,
 即①成立
即①成立当0<x≤1时,原不等式变为
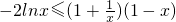 ,
,即
 ②
②由(1)结论0<x≤1时,f(x)≥f(1)=0,
 即②成立
即②成立综上得,所求不等式的解集是{x|x>0}
(3)结论:a的最大值为
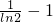 .
.证明:∵n∈N*,
∴
 ,
,∵
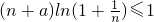 ,
,∴
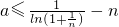 ,取
,取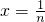 ,则x∈(0,1],
,则x∈(0,1],∴
 ,
,设
 ,
,则
 ,∴g(x)在x∈(0,1]上单调递减,
,∴g(x)在x∈(0,1]上单调递减,∴当x=1时,
 .
.∴a的最大值为
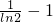 .
.分析:(1)利用导数即可求出其单调区间;
(2)通过对x讨论,再利用(1)的结论即可;
(3)通过分离参数,通过换元求导,再利用(1)的结论即可得出.
点评:熟练掌握利用导数研究函数的单调性、分离参数法和换元法是解题的关键.

练习册系列答案
相关题目



 的极值点;
的极值点; 过点(0,—1),并且与曲线
过点(0,—1),并且与曲线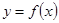 相切,求直线
相切,求直线 ,其中
,其中 ,求函数
,求函数 在
在 上的最小值.(其中e为自然对数的底数)
上的最小值.(其中e为自然对数的底数)