题目内容
如图,已知ABCD是正方形，BE∥AC，AC=CE，EC的延长线交BA的延长线于点F，求证：AF=AE.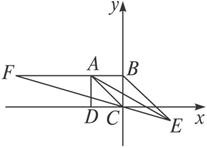
证明:以正方形ABCD的边DC所在的直线为x轴，以点C为坐标原点建立直角坐标系，设正方形的边长为1，则点A、B的坐标分别为A（-1，1）、B（0，1）.又设点E的坐标为（x,y),则
=（x,y-1),
=(1,-1).
∵
∥
,
∴x(-1)-1·（y-1)=0,
即x+y=1.①
又CE=AC,
∴x2+y2=2.②
∵点E在y轴右侧，
∴由①②得点E的坐标为(
).
∴|AE|=
.
再设点F的坐标为（x′,1),则
=(x′,1).
又
=(
)且
∥
，
∴
x′-
·1=0.
∴x′=-2-
.
∴F(-2-
,1).
从而|AF|=|-1-（-2-
）|=
+1.
∴AF=AE.
练习册系列答案
相关题目
如图，已知ABCD是边长为a的正方形，E，F分别是AB，AD的中点，CG⊥面ABCD，CG=a．
如图，已知ABCD是底角为30°的等腰梯形，AD=2
如图，已知ABCD是边长为1的正方形，AF⊥平面ABCD，CE∥AF，CE=λAF（λ＞1）．
如图，已知ABCD是矩形，PD⊥平面ABCD，PB=2，PB与平面ABCD所成的角为30°，PB与平面PCD所成的角为45°，求：
如图，已知ABCD是正方形，DE⊥平面ABCD，BF⊥平面ABCD，且AB=FB=2DE．