题目内容
9.设△ABC的内角A,B,C所对的边分别为a,b,c,且A=60°,b=1,c=3.(1)求a的值;
(2)求$\frac{1}{tanB}$+$\frac{1}{tanC}$的值.
分析 (1)利用余弦定理求a的值;
(2)由正弦定理可得sinB=$\frac{\sqrt{3}}{2\sqrt{7}}$,sinC=$\frac{3\sqrt{3}}{2\sqrt{7}}$,再求$\frac{1}{tanB}$+$\frac{1}{tanC}$的值.
解答 解:(1)∵A=60°,b=1,c=3,
∴a=$\sqrt{1+9-2×1×3×\frac{1}{2}}$=$\sqrt{7}$;
(2)由正弦定理可得$\frac{\sqrt{7}}{\frac{\sqrt{3}}{2}}=\frac{1}{sinB}=\frac{3}{sinC}$,∴sinB=$\frac{\sqrt{3}}{2\sqrt{7}}$,sinC=$\frac{3\sqrt{3}}{2\sqrt{7}}$
$\frac{1}{tanB}$+$\frac{1}{tanC}$=$\frac{cosB}{sinB}$+$\frac{cosC}{sinC}$=$\frac{sin(B+C)}{sinBsinC}$=$\frac{\sqrt{3}}{2}•\frac{2\sqrt{7}}{\sqrt{3}}•\frac{2\sqrt{7}}{3\sqrt{3}}$=$\frac{14\sqrt{3}}{9}$.
点评 本题考查余弦定理、正弦定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
20.已知P是△ABC所在平面外一点,若P到ABC三边距离相等,则点P在平面ABC上的射影一定是△ABC的( )
| A. | 重心 | B. | 外心 | C. | 内心 | D. | 垂心 |
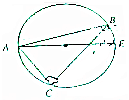 如图,已知,AE是⊙O的直径,弦BC与AE相交于D,求证:tanB•tanC=$\frac{AD}{DE}$.
如图,已知,AE是⊙O的直径,弦BC与AE相交于D,求证:tanB•tanC=$\frac{AD}{DE}$.