题目内容
【题目】已知递增数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,![]() .
.
(1)求证:数列![]() 为等差数列;
为等差数列;
(2)试求所有的正整数![]() ,使得
,使得![]() 为整数;
为整数;
(3)证明: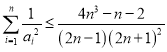 .
.
【答案】(1)见解析(2)![]() (3)见解析
(3)见解析
【解析】
(1)根据![]() ,得出
,得出![]() ,利用
,利用![]() ,即可得出
,即可得出![]() ,
,![]() 或
或![]() ,再结合题意
,再结合题意![]() 为递增数列,确定得
为递增数列,确定得![]() ,结合等差数列定义法,即可证出数列
,结合等差数列定义法,即可证出数列![]() 为等差数列;
为等差数列;
(2)由(1)知,数列![]() 为等差数列,首项为
为等差数列,首项为![]() ,公差
,公差![]() ,则
,则![]() ,化简得
,化简得![]() ,结合
,结合![]() 和
和![]() ,则
,则![]() 且
且![]() 为奇数,即可求出正整数
为奇数,即可求出正整数![]() ;
;
(3)由![]() ,利用放缩法和裂项相消法求和得出
,利用放缩法和裂项相消法求和得出![]() ,进而得出
,进而得出![]() ,要证
,要证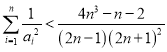 ,则需证
,则需证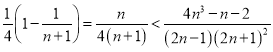 ,转化为证
,转化为证![]() ,
,
当![]() 时,上式显然成立,
时,上式显然成立,![]() 时,原不等式左边为
时,原不等式左边为![]() ,原不等式右边为
,原不等式右边为![]() ,则原不等式成立,从而即可证明
,则原不等式成立,从而即可证明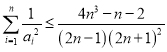 .
.
解:(1)由题可知,![]() ,
,![]() ,
,
则![]() ①,
①,
得![]() ②,
②,
由①-②得:![]() ,
,
即:![]() ,
,
即:![]() ,
,
所以![]() 或
或![]() ,
,
即:![]() 或
或![]() ,
,
若![]() ,则有
,则有![]() ,而
,而![]() ,所以
,所以![]() ,
,
即![]() ,这与数列
,这与数列![]() 递增矛盾,所以
递增矛盾,所以![]() 应舍去,
应舍去,
所以![]() ,故数列
,故数列![]() 为等差数列.
为等差数列.
(2)由(1)知,数列![]() 为等差数列,首项为
为等差数列,首项为![]() ,公差
,公差![]() ,
,
则![]() ,
,
故:![]()
![]()
![]() ,
,
即![]() ,
,
因为![]() ,所以
,所以![]() ,
,
由于![]() ,则
,则![]() 且
且![]() 为奇数,
为奇数,
所以![]() ,故
,故![]() .
.
(3)由(2)可知,![]() ,则
,则![]() ,
,
由于![]() ,
,
即:![]()
所以![]()
即:![]() ,
,
要证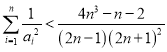 ,则需证
,则需证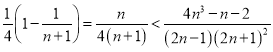 ,
,
即证:![]() ,
,
化为:![]() ,
,
即为:![]() ,
,
当![]() 时,上式显然成立,即
时,上式显然成立,即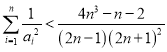 成立,
成立,
又![]() 时,原不等式左边
时,原不等式左边![]() ,原不等式右边
,原不等式右边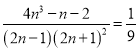 ,则原不等式成立,
,则原不等式成立,
所以综上可得: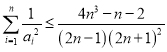 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


