题目内容
已知函数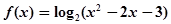 ,给定区间E,对任意
,给定区间E,对任意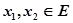 ,当
,当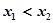 时,总有
时,总有 则下列区间可作为E的是( )
则下列区间可作为E的是( )
A.(-3,-1) B.(-1,0) C.(1,2) D.(3,6)
【答案】
A
【解析】
试题分析:根据题意由于函数 ,同时,任意
,同时,任意 ,当
,当 时,总有
时,总有 则说明函数在定义域内是递减的,因此求解的是函数的减区间,外层是递增的,则求解内层的减区间即可,对称轴x=1,那么开口向上,故可知答案为A.
则说明函数在定义域内是递减的,因此求解的是函数的减区间,外层是递增的,则求解内层的减区间即可,对称轴x=1,那么开口向上,故可知答案为A.
考点:函数的单调性
点评:解决的关键是根据给定的单调性的定义来判定函数的单调性,进而得到对应的复合函数 单调区间,属于基础题。

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
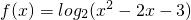 ,给定区间E,对任意x1,x2∈E,当x1<x2时,总有f(x1)>f(x2),则下列区间可作为E的是
,给定区间E,对任意x1,x2∈E,当x1<x2时,总有f(x1)>f(x2),则下列区间可作为E的是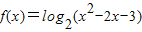 ,给定区间E,对任意x1,x2∈E,当x1<x2时,总有f(x1)>f(x2),则下列区间可作为E的是( )
,给定区间E,对任意x1,x2∈E,当x1<x2时,总有f(x1)>f(x2),则下列区间可作为E的是( )