题目内容

已知n∈N*，则
C
38-n
3n
+
C
3n
21+n
的值为
 
；（填数字）
分析：由题意可得 0≤38-n≤3n，且 0≤3n≤21+n，由此求得正整数n的值，从而求得
C
38-n
3n
+
C
3n
21+n
 的值．
解答：解：由题意可得 0≤38-n≤3n，且 0≤3n≤21+n，
解得
38
4
≤n≤
21
2
．
再根据 n∈N*，可得n=10，
故
C
38-n
3n
+
C
3n
21+n
=
C
2
30
+
C
1
31
=
30×29
2×1
+31=435+31=466，
故答案为：466．
点评：本题主要考查组合数的定义和性质应用，组合数的计算公式，属于基础题．
练习册系列答案
相关题目
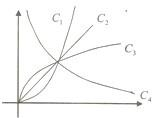
图中曲线是幂函数y=xn在第一象限的图象．已知n取±2，±
1
2
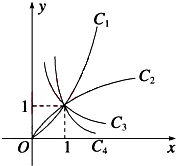
四个值，则相应于曲线c1、c2、c3、c4的n依次为（　　）精英家教网
A、-2，-
1
2
，
1
2
，2
B、2，
1
2
，-
1
2
，-2
C、-
1
2
，-2，2，
1
2
D、2，
1
2
，-2，-
1
2
精英家教网如图所示的曲线是幂函数y=xn在第一象限内的图象．已知n分别取-1，l，
1
2
，2四个值，则与曲线C1，C2，C3，C4相应的n依次为（　　）
A、2，1，
1
2
，-1
B、2，-1，1，
1
2
C、
1
2
，1，2，-1
D、-1，1，2，
1
2
已知两个正数a、b．则
a+b
2
≤
a2+b2
2
．三个正数a、b、c，则
a+b+c
3
≤
a2+b2+c2
3
；…类比写出n个正数的关系式并加以证明．
精英家教网图中曲线是幂函数y=xn在第一象限的图象，已知n取±3，±
1
3
四个值，则相应于曲线C1，C2，C3，C4的n依次为（　　）
A、-3，-
1
3
，
1
3
，3
B、3，
1
3
，-
1
3
，-3
C、-
1
3
，-3，3，
1
3
D、3，
1
3
，-3，-
1
3
图中曲线是幂函数y=xn在第一象限的图象，已知n取±2，±四个值，则相应于曲线C1，C2,C3,C4的n依次为(    )

A.-2,- ,,2                            B.2, ,-,-2

C.- ,-2,2,                            D.2, ,-2,-

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网