题目内容
如图所示，PA⊥平面ABCD，底面ABCD为菱形，∠ABC=60°，PA=AB=2，N为PC的中点．
（1）求证：BD⊥平面PAC；
（2）求二面角B-AN-C的正切值．
（1）求证：BD⊥平面PAC；
（2）求二面角B-AN-C的正切值．
（1）证明：ABCD是菱形 ，又PA⊥平面ABCD，BD  平面ABCD，∴BD⊥PA， 又PA∩AC=A， ∴BD⊥平面PAC。 |
|
| （2）解：由(l)可知，BO⊥平面PAC， 故在平面PAC内，作OM⊥AC，连结BM（如图）， 则∠BMO为二面角B-AN-C的平面角， 在Rt△BMO中，易知  ，∴  ，即二面角B-AN-C的正切值为  |
 |
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
如图所示，PA⊥平面ABCD，底面ABCD为菱形，∠ABC=60°，PA=AB=2，N为PC的中点．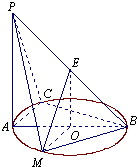
如图所示，PA⊥平面ABC，点C在以AB为直径的⊙O上，∠CBA=30°，PA=AB=2，，点E为线段PB的中点，点M在AB弧上，且OM∥AC．
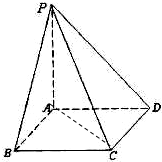如图所示，PA⊥平面ABCD，底面ABCD为直角梯形，
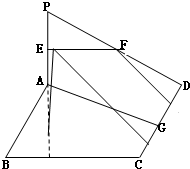如图所示，PA⊥平面ABCD，四边形ABCD为正方形，且2PA=AD=2，E、F、G分别是线段PA、PD、CD的中点．
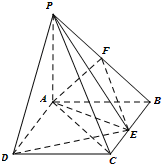如图所示，PA⊥平面ABCD，ABCD是边长为1的正方形．点F是PB的中点，点E在边BC上移动．