题目内容
平面直角坐标系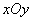 中,过椭圆
中,过椭圆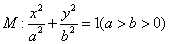 右焦点的直线
右焦点的直线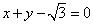 交
交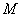 于
于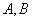 两点,
两点,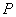 为
为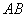 的中点,且
的中点,且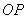 的斜率为
的斜率为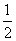 .
.
(Ⅰ)求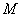 的方程;
的方程;
(Ⅱ)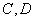 为
为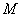 上的两点,若四边形
上的两点,若四边形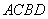 的对角线
的对角线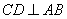 ,求四边形ACBD面积的最大值.
,求四边形ACBD面积的最大值.
解 (Ⅰ)设A (x 1, y 1) ,B (x 2, y 2),P (x 0, y 0)
⇒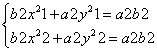 ⇒
⇒ 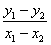 =
= 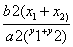 ⇒ kAB =
⇒ kAB = 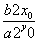
OP的斜率为 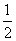 ⇒
⇒  = 2,直线x + y
= 2,直线x + y 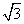 = 0的斜率为1 ⇒ kAB =1
= 0的斜率为1 ⇒ kAB =1
⇒1= 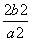 ⇒ a2 = 2b2 ……①
⇒ a2 = 2b2 ……①
由题意知直线x + y 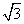 = 0与x轴的交点F(
= 0与x轴的交点F(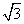 ,0)是椭圆的右焦点,则才c =
,0)是椭圆的右焦点,则才c = 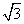
⇒a2 b2 = 3 ……②
联立解得①、②解得a2 = 6,b2 = 3
所以M的方程为: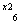 +
+ 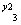 = 1
= 1
(Ⅱ)联立方程组 ,解得A(
,解得A(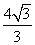 ,
, 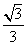 )、B(0,
)、B(0, 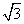 ),求得| AB | =
),求得| AB | = 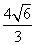
依题意可设直线CD的方程为:y = x + m
CD与线段AB相交⇒ 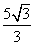 < m <
< m < 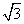
联立方程组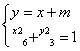 消去x得:3x 2 + 4mx +2m2 6 = 0 …… (*)
消去x得:3x 2 + 4mx +2m2 6 = 0 …… (*)
设C (x 3, y 3),D (x 4, y 4),则| CD |2 = 2(x 3 x 4)2 = 2[(x 3 + x 4)2 4x 3x 4]= 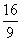 (9 m2)
(9 m2)
四边形ACBD的面积S = 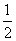 | AB |• | CD | =
| AB |• | CD | = 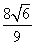
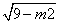
当n = 0时,S最大,最大值为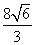 .
.
所以四边形ACBD的面积最大值为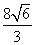 .
.

练习册系列答案
相关题目
 ,那么内角C等于 ( )
,那么内角C等于 ( ) 的一条渐近线与抛物线
的一条渐近线与抛物线 只有一个公共点,且该双曲线的一个焦点为F(c,0)则
只有一个公共点,且该双曲线的一个焦点为F(c,0)则
 。
。 ,
, ,若直线
,若直线 与圆
与圆 相切,则
相切,则 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.
 ,
, ,则
,则 。
。 与曲线
与曲线 有两个不同的交点,则
有两个不同的交点,则 的取值范围为 。
的取值范围为 。 在点
在点 处的切线与两条坐标轴围成的三角形的面积为54,则
处的切线与两条坐标轴围成的三角形的面积为54,则 ( )
( )  α,m
α,m