题目内容
一船以每小时15km的速度向东航行,船在A处看到一个灯塔B在北偏东60°,行驶4h后,船到达C处,看到这个灯塔在北偏东15°,这时船与灯塔的距离为多少km( )
分析:设过B点的南北方向直线与直线AB交于点D,且CD=xkm,结合题中数据在Rt△BCD中算出BD=(2+
)xkm,然后在Rt△ADB中算出AD=(2
+3)x,根据AC=AD-CD=15×4=60km建立关于x的方程解出x=15(
-1)km,最后在Rt△BCD中利用三角函数的定义加以计算,即可算出此时的船与灯塔的距离.
| 3 |
| 3 |
| 3 |
解答: 解:设根据题意,可得
解:设根据题意,可得
Rt△BCD中,设CD=xkm,
∵∠CBD=15°,∴tan∠CBD=
=(2-
)x
由此可得BD=
=(2+
)xkm
∵Rt△ADB中,∠ABD=60°
∴AD=
BD=(2
+3)x
因此,AC=AD-CD=(2
+3)x-x=15×4
即(2
+2)x=60,解之得x=15(
-1)km
由此可得Rt△BCD中,BC=
=
=30
km,即此时的船与灯塔的距离为30
km
故选:B
 解:设根据题意,可得
解:设根据题意,可得Rt△BCD中,设CD=xkm,
∵∠CBD=15°,∴tan∠CBD=
| CD |
| BD |
| 3 |
由此可得BD=
| CD | ||
2-
|
| 3 |
∵Rt△ADB中,∠ABD=60°
∴AD=
| 3 |
| 3 |
因此,AC=AD-CD=(2
| 3 |
即(2
| 3 |
| 3 |
由此可得Rt△BCD中,BC=
| CD |
| sin15° |
15(
| ||||||
|
| 2 |
| 2 |
故选:B
点评:本题给出实际应用问题,求航行过程中船与灯塔的距离.着重考查了利用正余弦定理解三角形、直角三角形中三角函数的定义和方位角的概念等知识,属于中档题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
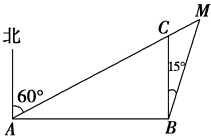 一船以每小时15km的速度向东航行,船在A处看到一灯塔M在北偏东60°方向,行驶4h后,船到达B处,看到这个灯塔在北偏东15°方向,这时船与灯塔的距离为
一船以每小时15km的速度向东航行,船在A处看到一灯塔M在北偏东60°方向,行驶4h后,船到达B处,看到这个灯塔在北偏东15°方向,这时船与灯塔的距离为 ,行驶
,行驶 后,船到达C处,看到这个灯塔在北偏东
后,船到达C处,看到这个灯塔在北偏东 ,这时船与灯塔距离为__________km.
,这时船与灯塔距离为__________km.