题目内容
一船以每小时15km的速度向东航行，船在A处看到一个灯塔B在北偏东60°，行驶4h后，船到达C处，看到这个灯塔在北偏东15°，求这时船与灯塔的距离？
分析：依题意，利用正弦定理即可求得船与灯塔的距离．
解答：
解：依题意，作图如图：
∵AC=15×4=60（km），在△ABC中，∠ABC=45°，∠BAC=30°，设BC=x（km），
根据正弦定理得：
=
，
即
=
，
∴x=
=30
．（km）
答：这时船与灯塔的距离为30
km．
解：依题意，作图如图：∵AC=15×4=60（km），在△ABC中，∠ABC=45°，∠BAC=30°，设BC=x（km），
根据正弦定理得：
| |AC| |
| sin∠ABC |
| |BC| |
| sin∠BAC |
即
| 60 |
| sin45° |
| x |
| sin30° |
∴x=
| 60sin30° |
| sin45° |
=30
| 2 |
答：这时船与灯塔的距离为30
| 2 |
点评：本题考查这正弦定理，考查两角和的正弦与根式运算，考查分析与运算能力，属于中档题．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
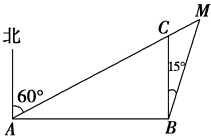一船以每小时15km的速度向东航行，船在A处看到一灯塔M在北偏东60°方向，行驶4h后，船到达B处，看到这个灯塔在北偏东15°方向，这时船与灯塔的距离为
，行驶
后，船到达C处，看到这个灯塔在北偏东
，这时船与灯塔距离为__________km.