题目内容
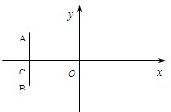 如图,在直角坐标系中,O为坐标原点,直线AB⊥x轴与点C,|
如图,在直角坐标系中,O为坐标原点,直线AB⊥x轴与点C,|| OC |
| CD |
| DO |
(I)求点M的轨迹方程
(II)设点K为点M的轨迹与x轴正半轴的交点,直线l交点M的轨迹于E,F两点(E,F与点K不重合),且满足
| KE |
| KF |
| OP |
| OE |
| OF |
分析:(I)欲求点M的轨迹方程,由椭圆的定义知动点M的轨迹是以点D为焦点、直线AB为其相应准线,离心率为
的椭圆,只须求出其a,b,c即可.
(II)先设设直线EF的方程为x=my+n,代入椭圆方程得到关于y的一元二次方程,利用根与系数的关系结合向量条件求得n的值,再利用向量关系式表示出直线KP的斜率,最后求出斜率的取值范围.
| 1 |
| 2 |
(II)先设设直线EF的方程为x=my+n,代入椭圆方程得到关于y的一元二次方程,利用根与系数的关系结合向量条件求得n的值,再利用向量关系式表示出直线KP的斜率,最后求出斜率的取值范围.
解答:解:(I)依题意知,点M的轨迹是以点D为焦点、
直线AB为其相应准线,离心率为
的椭圆
设椭圆的长轴长为2a,短轴长为2b,焦距为2c,
又|
|=4,
=3
,
∴点D在x轴上,且
=3,则
-c=3
解之得:a=2,c=1,b=
.
∴坐标原点O为椭圆的对称中心.
∴动点M的轨迹方程为:
+
=1;(4分)
(II)设E(x1,y1),F(x2,y2),
设直线EF的方程为x=my+n,
代入
+
=1得(3m2+4)y2+6mny+3n2-12=0.(5分)
△=36m2n2-12(3m2+4)(n2-4),
y1+y2=-
,y1y2=
.x1+x2=m(y1+y2)+2n=
,x1x2=
(6分)
∵
⊥
,∴(x1-2)(x2-2)+y1y2=0,
∴
=0,∴7n2-16n+4=0.
解得:n=
,n=2(舍).(8分)
设P(x0,y0),由2
=
+
知,
x0=
,y0=
.
直线KP的斜率为k=
=
.(10分)
当m=0时,k=0;
当m≠0时,k=
,
∵7m+
≥4
(m=
时取“=”)
或7m+
≤-4
(m=-
时取“=”),
∴k∈[-
,0)∪(0,
](12分)
综上所述k∈[-
,
].(13分)
直线AB为其相应准线,离心率为
| 1 |
| 2 |
设椭圆的长轴长为2a,短轴长为2b,焦距为2c,
又|
| OC |
| CD |
| DO |
∴点D在x轴上,且
| CD |
| a2 |
| c |
解之得:a=2,c=1,b=
| 3 |
∴坐标原点O为椭圆的对称中心.
∴动点M的轨迹方程为:
| x2 |
| 4 |
| y2 |
| 3 |
(II)设E(x1,y1),F(x2,y2),
设直线EF的方程为x=my+n,
代入
| x2 |
| 4 |
| y2 |
| 3 |
△=36m2n2-12(3m2+4)(n2-4),
y1+y2=-
| 6mn |
| 3m2+4 |
| 3n2-12 |
| 3m2+4 |
.x1+x2=m(y1+y2)+2n=
| 8n |
| 3m2+4 |
| 4n2-12m2 |
| 3m2+4 |
∵
| KE |
| KF |
∴
| 4n2-12m2-16n+12m2+16+3n2-12 |
| 3m2+4 |
解得:n=
| 2 |
| 7 |
设P(x0,y0),由2
| OP |
| OE |
| OF |
x0=
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
直线KP的斜率为k=
| y0 |
| x0-2 |
| m |
| 7m2+8 |
当m=0时,k=0;
当m≠0时,k=
| 1 | ||
7m+
|
∵7m+
| 8 |
| m |
| 14 |
|
或7m+
| 8 |
| m |
| 14 |
|
∴k∈[-
| 1 | ||
4
|
| 1 | ||
4
|
综上所述k∈[-
| ||
| 56 |
| ||
| 56 |
点评:本小题主要考查曲线与方程,直线和圆锥曲线,向量的运算等基础知识,以及求最值的基本技能和综合运用数学知识解决问题的能力.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
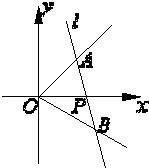 如图,在直角坐标系中,射线OA:x-y=0(x≥0),OB:
如图,在直角坐标系中,射线OA:x-y=0(x≥0),OB: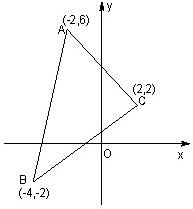 如图,在直角坐标系中,已知△ABC的三个顶点的坐标,求:
如图,在直角坐标系中,已知△ABC的三个顶点的坐标,求: 如图,在直角坐标系中,直线y=6-x与
如图,在直角坐标系中,直线y=6-x与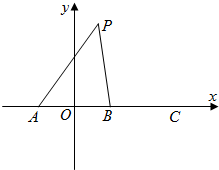 如图,在直角坐标系中,A,B,C三点在x轴上,原点O和点B分别是线段AB和AC的中点,已知AO=m(m为常数),平面上的点P满足PA+PB=6m.
如图,在直角坐标系中,A,B,C三点在x轴上,原点O和点B分别是线段AB和AC的中点,已知AO=m(m为常数),平面上的点P满足PA+PB=6m.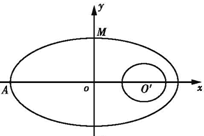 如图,在直角坐标系中,中心在原点,焦点在x轴上的椭圆G的离心率为
如图,在直角坐标系中,中心在原点,焦点在x轴上的椭圆G的离心率为