题目内容
已知△ABC的面积为6,三边a,b,c所对的角为A,B,C,若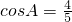 ,且b-c=1,则a的值为
,且b-c=1,则a的值为
- A.3
- B.4
- C.5
- D.6
A
分析:由cosA的值,及A为三角形的内角,利用同角三角函数间的基本关系求出sinA的值,再根据三角形的面积为6,利用三角形的面积公式得出bc的值,再由b-c的值,两者联立求出b与c的值,再由cosA的值,利用余弦定理即可求出a的值.
解答:∵cosA= ,A为三角形的内角,
,A为三角形的内角,
∴sinA=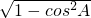 =
= ,
,
又△ABC的面积为6,
∴S= bcsinA=6,即
bcsinA=6,即 bc=6,
bc=6,
∴bc=20,又b-c=1,
解得:b=5,c=4,
∴由余弦定理得:a2=b2+c2-2bccosA=25+16-32=9,
则a=3.
故选A
点评:此题考查了余弦定理,三角形的面积公式,以及同角三角函数间的基本关系,熟练掌握定理及公式是解本题的关键.
分析:由cosA的值,及A为三角形的内角,利用同角三角函数间的基本关系求出sinA的值,再根据三角形的面积为6,利用三角形的面积公式得出bc的值,再由b-c的值,两者联立求出b与c的值,再由cosA的值,利用余弦定理即可求出a的值.
解答:∵cosA=
 ,A为三角形的内角,
,A为三角形的内角,∴sinA=
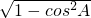 =
= ,
,又△ABC的面积为6,
∴S=
 bcsinA=6,即
bcsinA=6,即 bc=6,
bc=6,∴bc=20,又b-c=1,
解得:b=5,c=4,
∴由余弦定理得:a2=b2+c2-2bccosA=25+16-32=9,
则a=3.
故选A
点评:此题考查了余弦定理,三角形的面积公式,以及同角三角函数间的基本关系,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目
 如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使
如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使 (2012•温州一模)如图,在△ABC中,AD⊥BC,垂足为D,且BD:DC:AD=2:3:6.
(2012•温州一模)如图,在△ABC中,AD⊥BC,垂足为D,且BD:DC:AD=2:3:6.