题目内容
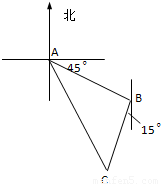
 如图,甲船在A处,乙船在A处的南偏东45°方向,距A有9n mile并以20n mile/h的速度沿南偏西15°方向航行,若甲船以28n mile/h的速度航行,用多少小时能尽快追上乙船?
如图,甲船在A处,乙船在A处的南偏东45°方向,距A有9n mile并以20n mile/h的速度沿南偏西15°方向航行,若甲船以28n mile/h的速度航行,用多少小时能尽快追上乙船?
分析:先利用平面中的知识求出∠ABC=180°-45°-15°=120°.再利用余弦定理AC2=AB2+BC2-2AB•BCcosα,即可求出对应的时间.
解答:解:设用th,甲船能追上乙船,且在C处相遇.
在△ABC中,AC=28t,BC=20t,AB=9,设∠ABC=α,∠BAC=β.
∴α=180°-45°-15°=120°.
根据余弦定理AC2=AB2+BC2-2AB•BCcosα,
(28t)2=81+(20t)2-2×9×20t×(-
),
128t2-60t-27=0,(4t-3)(32t+9)=0,
解得t=
,t=-
(舍)
即最快用
h可以追上乙船.
在△ABC中,AC=28t,BC=20t,AB=9,设∠ABC=α,∠BAC=β.
∴α=180°-45°-15°=120°.
根据余弦定理AC2=AB2+BC2-2AB•BCcosα,
(28t)2=81+(20t)2-2×9×20t×(-
| 1 |
| 2 |
128t2-60t-27=0,(4t-3)(32t+9)=0,
解得t=
| 3 |
| 4 |
| 9 |
| 32 |
即最快用
| 3 |
| 4 |
点评:本题主要考查解三角形的实际应用.解决这一类型题目的关键是把文字语言转化为数学符号,用数学公式,定理,公理等知识来解.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目

 倍,问:甲船应取什么方向才能追上乙船?追上时甲船行驶了多少海里?
倍,问:甲船应取什么方向才能追上乙船?追上时甲船行驶了多少海里?