题目内容
某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗A原料1千克、B原料2千克;生产乙产品1桶需耗A原料2千克,B原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗A、B原料都不超过12千克.公司如何合理安排生产计划,可使每天生产的甲、乙两种产品,共获得最大利润?
分析:根据题设中的条件可设每天生产甲种产品x桶,乙种产品y桶,根据题设条件得出线性约束条件以及目标函数求出利润的最大值即可.
解答: 解:设生产x桶甲产品,y桶乙产品,总利润为Z,
解:设生产x桶甲产品,y桶乙产品,总利润为Z,
则约束条件为
,目标函数为Z=300x+400y,
可行域如图
当目标函数直线经过点M时z有最大值,联立方程组
得M(4,4),代入目标函数得z=2800.
故公司每天生产的甲、乙两种产品各4桶,可获得最大利润2800元.
 解:设生产x桶甲产品,y桶乙产品,总利润为Z,
解:设生产x桶甲产品,y桶乙产品,总利润为Z,则约束条件为
|
可行域如图
当目标函数直线经过点M时z有最大值,联立方程组
|
故公司每天生产的甲、乙两种产品各4桶,可获得最大利润2800元.
点评:本题考查用线性规划知识求利润的最大值,这是简单线性规划的一个重要运用,解题的关键是准确求出目标函数及约束条件.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
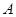 原料1千克、
原料1千克、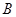 原料2千克;生产乙产品1桶需耗
原料2千克;生产乙产品1桶需耗