Question

【题目】已知数列{an}满足：an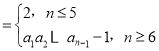（n∈N*）．若正整数k（k≥5）使得a12+a22+…+ak2＝a1a2…ak成立，则k＝（ ）

A.16B.17C.18D.19

Answer 1

【答案】B

【解析】

由题意可得a1＝a2＝a3＝a4＝a5＝2，a6＝a1a2a3…a5﹣1＝25﹣1＝31，n≥6时，a1a2…an﹣1＝1+an，将n换为n+1，两式相除整理得an2＝an+1﹣an+1，n≥6，求得a62+a72+…+ak2＝ak+1﹣a6+k﹣5，结合已知条件，即可得到所求值．

解：an（n∈N*），

即a1＝a2＝a3＝a4＝a5＝2，a6＝a1a2a3…a5﹣1＝25﹣1＝31，

n≥6时，a1a2…an﹣1＝1+an，所以a1a2…an＝1+an+1，

两式相除可得an，

则an2＝an+1﹣an+1，n≥6，

由a62＝a7﹣a6+1，

a72＝a8﹣a7+1，

…，

ak2＝ak+1﹣ak+1，k≥5，

可得a62+a72+…+ak2＝ak+1﹣a6+k﹣5

a12+a22+…+ak2＝20+ak+1﹣a6+k﹣5＝ak+1+k﹣16，

且a1a2…ak＝1+ak+1，

正整数k（k≥5）使得a12+a22+…+ak2＝a1a2…ak成立，

则ak+1+k﹣16＝ak+1+1，

则k＝17，

故选：B．