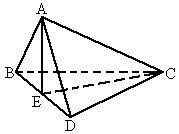
题目内容
如图，已知A是△BCD所在平面外一点，AB=AD，AB⊥BC，AD⊥DC，E为BD的中点．
求证：(1)平面AEC⊥平面ABD；
(2)平面AEC⊥平面BCD．
答案：略
解析：
解析：
|
证明 (1)在Rt△ABC与Rt△ADC中，∵AB=AD，∴BC=DC．∵ E为BD的中点，∴AE⊥BD，CE⊥BD．而 AE∩CE=E，∴BD⊥平面AEC．∵  ，∴平面AEC⊥平面ABD，
(2) ∵BD⊥平面AEC， ，
∴平面 AEC⊥平面BCD． |
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
