题目内容
已知函数
(Ⅰ)若 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.
(Ⅱ)若 的一个极值点,求
的一个极值点,求 上的最大值.
上的最大值.
【答案】
(I)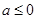 ;(II)
;(II)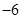 .
.
【解析】
试题分析:(I)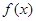 在
在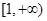 上是增函数,则其导数
上是增函数,则其导数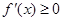 在
在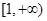 上恒成立.
上恒成立.
由于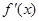 是二次函数,所以可结合图象寻找
是二次函数,所以可结合图象寻找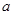 满足的不等式,从而求出
满足的不等式,从而求出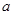 的取值范围.
的取值范围.
(II)依题意, 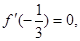 由此可求得
由此可求得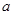 的值.进而求到
的值.进而求到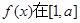 上的最大值.
上的最大值.
试题解析:(I)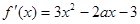
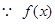 在
在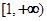 上是增函数,
上是增函数,
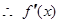 在
在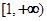 上恒有
上恒有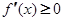 .
3分
.
3分
即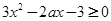 在
在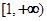 上恒成立.
上恒成立.
则必有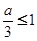 且
且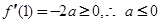 .
6分
.
6分
(II)依题意,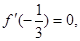
即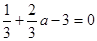
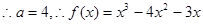 .
8分
.
8分
令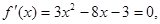
得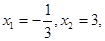 则
则
当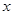 变化时,
变化时,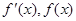 的变化情况如下表:
的变化情况如下表:
|
|
1 |
(1,3) |
3 |
(3,4) |
4 |
|
|
|
— |
0 |
+ |
|
|
|
—6 |
|
—18 |
|
—12 |
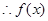 在[1,4]上的最大值是
在[1,4]上的最大值是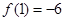 13分
13分
考点:导数的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
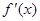

 上是增函数,求
上是增函数,求 的取值范围;
的取值范围; ;
; 

 上是增函数,求
上是增函数,求 的取值范围;
的取值范围; ;
; 