题目内容
【题目】在一个特定时段内，以点
为中心的
海里以内海域被设为警戒水域.点
正北
海里有一个雷达观测站
，某时刻测得一艘匀速直线行驶的船只位于点
北偏东
且与点相距
海里的位置
，经过
分钟又测得该船已行驶到点北偏东
（其中
且与点相距
海里的位置
.
（1）求该船的行驶速度（单位：海里/小时）；
（2）若该船不改变航行方向继续行驶，判断它是否会进入警戒水域，并说明理由.
【答案】（1）
（海里/小时）；（2）船会进入警戒水域，理由见解析．
【解析】
试题分析：（1）先根据题意画出简图确定
的值，根据
球场
的余弦值，再由余弦定理求出
的值，从而可得到船的行驶速度；（2）设直线
与
的延长线相交于点
.根据余弦定理求出
的值，进而可得到其正弦值，再由正弦定理可得
的长度，从而可确定
在点
和点
之间，根据
求出
的长度，然后过点
作
，则
为点
到直线
的距离，进而在
中求出
的值，进行比较可得得到答案.
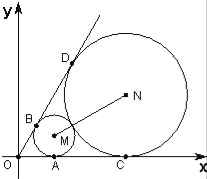
试题解析：（1）如图，
，
由于
，所以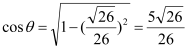
.
由余弦定理得
，
所以船的行驶速度为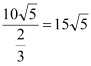
（海里/小时）.
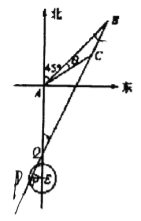
（2）如图所示，设直线与的延长线相交于点.在
中，
由余弦定理得，
，
从而
.
在
中，由正弦定理得，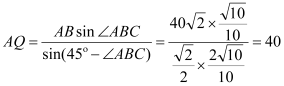
，
由于
，所以点
位于点
和点
之间，且
.
过点
作
于点
，则
为点
到直线的距离.
在
中，
，
所以船会进入警戒水域.
练习册系列答案
相关题目
【题目】某班主任对全班50名学生作了一次调查，所得数据如表：
认为作业多 | 认为作业不多 | 总计 | |
喜欢玩电脑游戏 | 18 | 9 | 27 |
不喜欢玩电脑游戏 | 8 | 15 | 23 |
总计 | 26 | 24 | 50 |
由表中数据计算得到K2的观测值k≈5.059，于是________（填“能”或“不能”）在犯错误的概率不超过0.01的前提下认为喜欢玩电脑游戏与认为作业多有关．