题目内容
设函数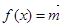 ·
·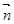 ,其中向量
,其中向量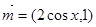 ,
,
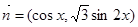 ,
,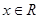 。
。
(1)求f (x)的最小正周期与单调递减区间;
(2)在△ABC中,a、b、c分别是角A、B、C的对边,已知f (A) =2,b = 1,
△ABC的面积为 ,求△ABC 外接圆半径R的值。
,求△ABC 外接圆半径R的值。
【答案】
(1)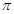 ,
,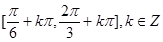 (2)R=1
(2)R=1
【解析】本试题主要是考查了三角函数的性质和解三角形的综合运用。
(1)先根据向量的数量积运算表示出函数f(x),再由二倍角公式和两角和与差的公式进行化简,根据T公式可求得最小正周期,再由正弦函数的单调性可求得单调递增区间.
(2)由f(A) = 2,得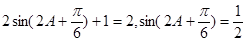 ,
,
在△ABC中,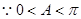 ,
,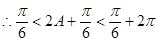 ,
,
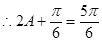 ,解得
,解得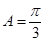 ,表示面积得到。
,表示面积得到。
解:(1)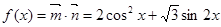
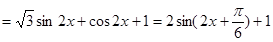 ,
,
∴函数f(x)的最小正周期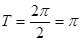 。............3分
。............3分
令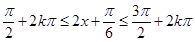
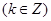 ,解得
,解得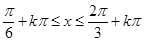 。
。
∴函数f(x)的单调递减区间是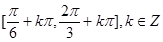 。........... 6分
。........... 6分
(2)由f(A) = 2,得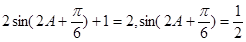 ,
,
在△ABC中,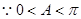 ,
,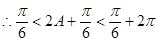 ,
,
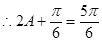 ,解得
,解得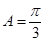 。
。
又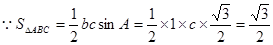 ,解得c = 2,
,解得c = 2,
△ABC中,由余弦定理得: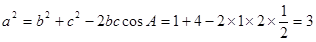 ,∴a =
,∴a = 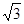
根据正弦定理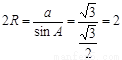 ,得R=1。............12分
,得R=1。............12分

练习册系列答案
相关题目
 ,
, ),
), =(
=(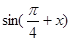
 ,
, ),x
),x R求:
R求: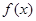 的解析式并进行化简;
的解析式并进行化简; 的方程
的方程 在
在 上有解,求实数
上有解,求实数 的取值范围。
的取值范围。